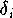 behaftet sind:
behaftet sind:
[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]
Im Standardfall der diskreten Approximation geht man von der Annahme aus,
daß nur die Werte der abhängigen Variablen y mit einem additiven Fehler
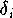 behaftet sind:
behaftet sind:
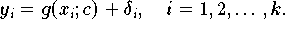
Falls die Fehler
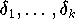 unabhängige Zufallsgrößen sind,
die alle normalverteilt sind mit dem Mittelwert Null und der Varianz
unabhängige Zufallsgrößen sind,
die alle normalverteilt sind mit dem Mittelwert Null und der Varianz
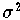 , dann ist die Maximum-Likelihood-Schätzung für den Parametervektor
, dann ist die Maximum-Likelihood-Schätzung für den Parametervektor
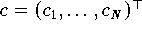 die Lösung des Approximationsproblems bzgl. der
die Lösung des Approximationsproblems bzgl. der
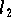 -Norm
-Norm
![\begin{eqnarray*}
D_2 (\Delta_k g^{*}, y) & = &
\min \{ D_2 (\Delta_k g, y): g \in {\cal G}_N \}\\
& & \mbox{mit}\quad D_2 (\Delta_k g, y) := \sqrt{ \sum \limits_{i=1}^{k}
[g(x_i;c) - y_i]^2}.
\end{eqnarray*}](pic/f04_0704.gif)
Der Parametervektor wird also in diesem Fall am besten nach der Methode der kleinsten Quadrate bestimmt, bei der der vertikale Abstand zwischen Datenpunkten und Approximationsfunktion "Euklidisch gemessen" wird.
In der Praxis sind aber Situationen durchaus nicht selten,
in denen auch die Werte
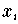 der unabhängigen Variablen - z.B. auf Grund von Meß-
oder Diskretisierungs-Ungenauigkeiten - additiv mit einem Fehler
der unabhängigen Variablen - z.B. auf Grund von Meß-
oder Diskretisierungs-Ungenauigkeiten - additiv mit einem Fehler
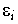 behaftet sind:
behaftet sind:
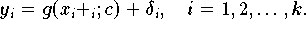
In solchen Fällen ist eine Abstandsdefinition angemessener, die den kürzesten,
d.h. den
orthogonalen Abstand
jedes Datenpunktes
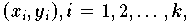 von der Approximationskurve (im univariaten Fall
von der Approximationskurve (im univariaten Fall
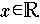 ) bzw. von der Approximationsfläche (im multivariaten Fall
) bzw. von der Approximationsfläche (im multivariaten Fall
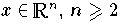 )
)
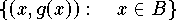
berücksichtigt.
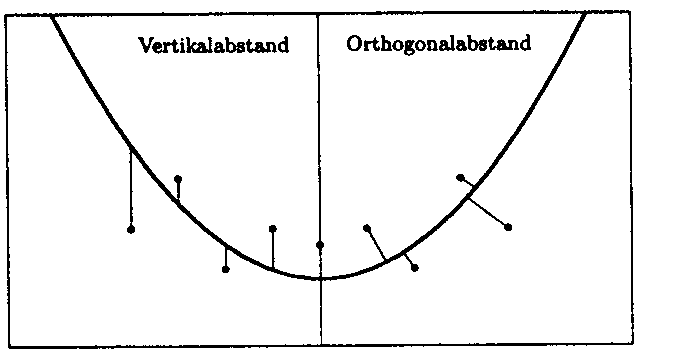
Abbildung: Vertikal- und Orthogonalabstände zwischen Datenpunkten
und einer Funktion.
Terminologie: Orthogonale Approximation
Die Bezeichnung für Methoden, die auf orthogonalen Abstandsdefinitionen beruhen, ist nicht einheitlich. So verwenden z.B. Golub und Van Loan [48] sowie Van Huffel und Vanderwalle [386] den Begriff "totale Methode der kleinsten Quadrate" (total least squares), während Powell und Macdonald [328] von der "verallgemeinerten Methode der kleinsten Quadrate" ( generalized least squares) sprechen.
Boggs, Byrd und Schnabel [121] verwenden den Begriff "Regression mit orthogonalen Abständen" ( orthogonal distance regression) und Ammann und Van Ness [86] "Orthogonale Regression" (orthogonal regression).
Der Begriff Regression wurde 1885 von F. Galton zur Charakterisierung von Erblichkeitseigenschaften eingeführt. Unter Regressionsanalyse versteht man heute in der Mathematischen Statistik Untersuchungen über stochastische Abhängigkeiten und deren funktionale Beschreibung anhand einer vorliegenden Stichprobe. Im Bereich der Numerischen Datenverarbeitung wird der Begriff Regression gelegentlich als Synonym für Approximation verwendet.
Achtung: Der Begriff "orthogonale Approximation" darf nicht verwechselt werden mit Approximation durch orthogonale Funktionen, d.h. Funktionen, die bezüglich eines inneren Produktes orthogonal zueinander sind (z.B. Tschebyscheff-Polynome, trigonometrische Polynome etc.).
Orthogonale Approximation ist nicht nur bei fehlerbehafteten unabhängigen Variablen der "gewöhnlichen" Approximation (mit Berücksichtigung von Vertikalabständen) vorzuziehen, sondern ist auch bei der Visualisierung (einer graphisch-darstellerisch orientierten Approximation) von Vorteil. Wenn man nur Vertikalabstände berücksichtigt, findet - hinsichtlich des optischen Eindrucks - eine stärkere Gewichtung steilerer Abschnitte des Funktionsverlaufs statt. Bei orthogonaler Approximation gibt es diese Art der Ungleichgewichtung nicht.
Neben der orthogonalen Approximation gibt es noch eine andere Möglichkeit zur Vermeidung der "visuellen" Ungleichgewichtung von Stellen mit geringer und großer Steigung: Die Parametrisierung der Daten und die anschließende Anpassung einer ebenen Kurve . Der Vorteil dieser Vorgangsweise - verglichen mit der orthogonalen Approximation - liegt im geringeren Aufwand, ihr Nachteil darin, daß die Approximationskurve unter Umständen keine Funktion mehr ist, also die Eindeutigkeit unter Umständen verlorengeht.
* * *
Im Umweltschutz wird von den vielen in der Luft vorhandenen Schadstoffen
nur eine geringe Anzahl regelmäßig gemessen.
Will man die Konzentrationswerte einer Substanz (z.B. SO2) als
Indikator für die Konzentration eines anderen Schadstoffes
(z.B. HCl) heranziehen, so muß man auf der Basis simultan durchgeführter
Konzentrationsmessungen beider Substanzen ein Modell entwickeln,
das den Zusammenhang beschreibt.
In diesem Fall liegen der Modellbildung Datenpunkte
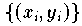 zugrunde,
bei denen die y-Werte und die x-Werte mit Meßfehlern behaftet sind.
zugrunde,
bei denen die y-Werte und die x-Werte mit Meßfehlern behaftet sind.
* * *
Die beiden Funktionen
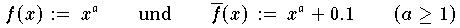
haben den konstanten vertikalen Abstand
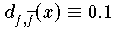 . Der orthogonale Abstand der Funktionen f und
. Der orthogonale Abstand der Funktionen f und
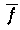 hängt jedoch sehr stark von x und a ab (siehe
folgende Abbildung).
hängt jedoch sehr stark von x und a ab (siehe
folgende Abbildung).
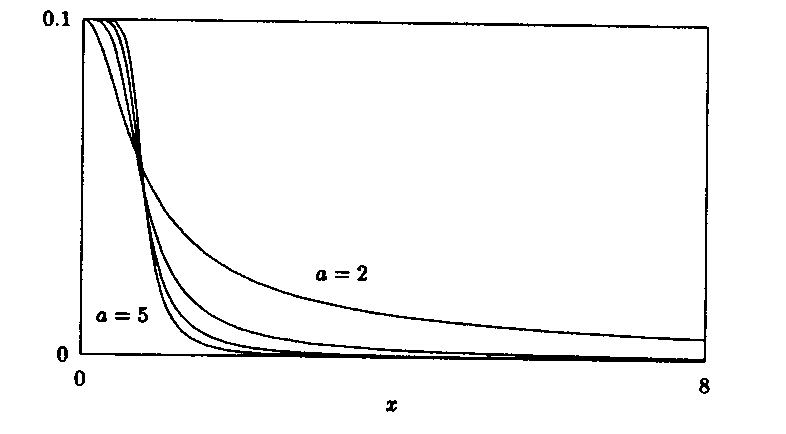
Abbildung:
Orthogonalabstände zwischen
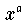 und
und
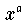 + 0.1.
+ 0.1.
Dies ist darauf zurückzuführen, daß die Steilheit des Funktionsverlaufs
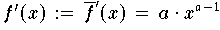
mit größeren Werten von x und a > 1 zunimmt.
[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]