[ < ]
[ globale Übersicht ]
[ Kapitelübersicht ]
[ Stichwortsuche ]
[ > ]
Robuste Abstandsmaße
Als robuste Verfahren bezeichnet man in der Statistik Verfahren,
die auch dann "vernünftige" Werte liefern,
wenn die Eigenschaften der Daten nicht jenen theoretischen Voraussetzungen entsprechen,
unter denen die Methode entwickelt bzw. optimiert wurde,
wenn z.B. die tatsächliche Verteilung der stochastischen Störungen
nicht jener Verteilung entspricht,
für die eine Methode optimale Eigenschaften (z.B. kleinste Varianz) besitzt.
Bei diskreten, aus Messungen stammenden Daten tritt immer wieder der
Fall ein, daß einzelne Werte - im Vergleich zu den übrigen
Datenpunkten, die mit stochastisch gleichartigen Störungen
(
"Rauschen"
) überlagert sind - in irgendeiner Weise verfälscht sind.
In diesem Fall liegt den stochastischen Störungen eine
Mischverteilung
zugrunde.
Werte, die als Realisierung der vorwiegend aufgetretenen stochastischen
Störung ("Rauschen") fraglich erscheinen, werden als
Ausreißer bezeichnet.
Beispiel: Scanner
In jeder Stichprobe aus einer Grundgesamtheit, die zu einer unbeschränkten
(z.B. normalverteilten) Zufallsgröße gehört,
sind beliebig große bzw. beliebig kleine Werte
(d.h. Werte oberhalb bzw. unterhalb jeder vorgegebenen Schranke)
mit positiver Wahrscheinlichkeit zu erwarten.
Deshalb ist das Erkennen und Ausscheiden von Ausreißern
("verdächtigen" Werten) nicht einfach.
Der Einfluß von Ausreißern auf die Lösung eines Approximationsproblems,
d.h. auf die Approximationsfunktion g,
hängt sehr stark von der gewählten Distanzfunktion
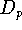 ab. Je größer p ist,
desto stärker wirken sich Ausreißer auf die Funktion g aus;
am stärksten selbstverständlich bei der Maximumnorm,
aber auch bei p = 2, bei der Euklidischen Norm,
oft immer noch unerwünscht stark.
Günstige Werte liegen etwa bei
ab. Je größer p ist,
desto stärker wirken sich Ausreißer auf die Funktion g aus;
am stärksten selbstverständlich bei der Maximumnorm,
aber auch bei p = 2, bei der Euklidischen Norm,
oft immer noch unerwünscht stark.
Günstige Werte liegen etwa bei
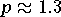 ([Ekblom [183]]).
([Ekblom [183]]).
Beispiel: Robuste Schätzung eines Skalars
Falls die stochastischen Störungen
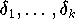 Realisierungen einer Normalverteilung mit dem Mittelwert Null sind,
dann liefert das Stichprobenmittel die optimale Schätzung für die
ungestörte Größe c,
da es unter allen linearen, erwartungstreuen Schätzfunktionen die kleinste Varianz besitzt.
Falls die Verteilungsfunktion der Störungen jedoch geringfügig von jener der Normalverteilung abweicht,
wenn z.B. eine Mischverteilung mit der Verteilungsfunktion
Realisierungen einer Normalverteilung mit dem Mittelwert Null sind,
dann liefert das Stichprobenmittel die optimale Schätzung für die
ungestörte Größe c,
da es unter allen linearen, erwartungstreuen Schätzfunktionen die kleinste Varianz besitzt.
Falls die Verteilungsfunktion der Störungen jedoch geringfügig von jener der Normalverteilung abweicht,
wenn z.B. eine Mischverteilung mit der Verteilungsfunktion
![\[
(1-\eps)\Phi + \eps H, \quad \eps \in [0,1],
\]](pic/f04_0602.gif)
vorliegt (
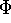 bezeichnet die Verteilungsfunktion der Normalverteilung und H
eine unbekannte Verteilungsfunktion),
dann kann mit wachsendem
bezeichnet die Verteilungsfunktion der Normalverteilung und H
eine unbekannte Verteilungsfunktion),
dann kann mit wachsendem
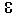 die Varianz des Stichprobenmittels
die Varianz des Stichprobenmittels
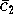 sehr schnell steigen.
sehr schnell steigen.
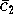 ist also (im statistischen Sinn) keine robuste Schätzfunktion,
während
ist also (im statistischen Sinn) keine robuste Schätzfunktion,
während
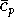 mit
mit
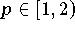 wesentlich weniger empfindlich auf Änderungen der Verteilungsfunktion reagiert.
wesentlich weniger empfindlich auf Änderungen der Verteilungsfunktion reagiert.
Der zentrale Grenzverteilungssatz liefert eine sehr allgemeine Aussage über
die Konvergenz der Verteilungsfunktion einer Summe unabhängiger
Zufallsgrößen gegen die Normalverteilung. Er wird sehr oft als
Rechtfertigung verwendet, wenn Zufallserscheinungen, die sich aus der
additiven Überlagerung einer Vielzahl zufälliger Einzeleffekte ergeben,
durch die Normalverteilung beschrieben werden.
Der zentrale Grenzverteilungssatz wurde damit zur Motivation für die bevorzugte Verwendung der
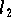 -Norm. Dabei erklärt er allenfalls,
warum viele in der Praxis auftretende Zufallsgrößen angenähert normalverteilt sind.
-Norm. Dabei erklärt er allenfalls,
warum viele in der Praxis auftretende Zufallsgrößen angenähert normalverteilt sind.
Historisch gesehen war für C. F. Gauß die Hauptmotivation für die
Verwendung der
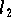 -Norm in seiner
Methode der kleinsten Quadrate
die einfache Berechenbarkeit
der "Ausgleichslösungen" aus linearen Gleichungssystemen.
-Norm in seiner
Methode der kleinsten Quadrate
die einfache Berechenbarkeit
der "Ausgleichslösungen" aus linearen Gleichungssystemen.
Erst seit den sechziger Jahren wird die Frage untersucht, was passiert,
wenn die Annahme einer Normalverteilung geringfügig gestört ist,
und wie man zu robusten Schätzverfahren gelangt.
Dabei stellte sich heraus, daß ein Ausgleich im Sinne der
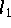 -Norm, aber auch mit
-Norm, aber auch mit
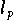 -Normen mit
-Normen mit
![$p \in (1,1.5]$](pic/f04_0609.gif) , zu robusteren,
wenngleich rechenaufwendigeren Schätzverfahren führt.
, zu robusteren,
wenngleich rechenaufwendigeren Schätzverfahren führt.
Die Maximumnorm (die
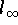 -Norm),
die zu Schätzungen führt,
die auf extreme Beobachtungen noch wesentlich empfindlicher reagiert als die entsprechenden
-Norm),
die zu Schätzungen führt,
die auf extreme Beobachtungen noch wesentlich empfindlicher reagiert als die entsprechenden
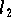 -Schätzungen, kommt für praktische Datenanalysen nicht in Frage.
(Bei der Funktionsapproximation hingegen wird fast immer die Maximumnorm verwendet.)
-Schätzungen, kommt für praktische Datenanalysen nicht in Frage.
(Bei der Funktionsapproximation hingegen wird fast immer die Maximumnorm verwendet.)
Die Wahl zwischen der
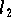 -Norm und einer
-Norm und einer
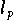 -Norm mit
-Norm mit
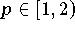 wird von zwei Faktoren beeinflußt:
wird von zwei Faktoren beeinflußt:
- Die
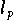 -Normen mit
-Normen mit
![$p \in [1,1.5]$](pic/f04_0611.gif) führen auf robuste Verfahren und sind aus diesem Grund der
führen auf robuste Verfahren und sind aus diesem Grund der
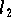 -Norm überlegen.
-Norm überlegen.
- Der Rechenaufwand für Verfahren der kleinsten Quadrate
(Approximation auf der Grundlage der
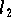 -Norm) ist deutlich geringer als bei anderen
-Norm) ist deutlich geringer als bei anderen
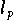 -Normen, da in diesem Fall nur lineare Gleichungssysteme zu lösen sind.
-Normen, da in diesem Fall nur lineare Gleichungssysteme zu lösen sind.
Bei "kleinen" Datenanalyseproblemen (mit einer kleinen Zahl von unbekannten Parametern),
wo der Rechenaufwand keine dominante Rolle spielt,
wird man - falls entsprechende Software vorhanden ist - Ausgleichsfunktionen im Sinne einer
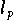 -Norm mit
-Norm mit
![$p \in [1,1.5]$](pic/f04_0611.gif) ermitteln.
Wo der Rechenaufwand jedoch von dominanter Bedeutung ist,
z.B. bei großen Ausgleichsproblemen
(mit hunderten oder tausenden Koeffizienten),
wird im allgemeinen aus Effizienzgründen die Methode der kleinsten Quadrate vorgezogen.
ermitteln.
Wo der Rechenaufwand jedoch von dominanter Bedeutung ist,
z.B. bei großen Ausgleichsproblemen
(mit hunderten oder tausenden Koeffizienten),
wird im allgemeinen aus Effizienzgründen die Methode der kleinsten Quadrate vorgezogen.
* * *
Beispiel
Scanner
Multispektrale Abtastsysteme (multispectral scanner) werden zur bildmäßigen Erfassung der Erdoberfläche,
z. B. im Rahmen von Umweltschutzprojekten in Satelliten, aber auch in (Propeller-) Flugzeugen eingesetzt.
Durch elektrische Einstreuungen aus der Umgebung des Scanners (Zündanlage der Motoren, Bordelektrik) können
punktförmige Störungen (spikes) - pixel mit minimalem oder maximalem Grauwert - in der digitalen
Bildverarbeitung auftreten.
* * *
Robuste Schätzung eines Skalars
Um den Einfluß von den Meßfehlern
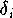 auf die Ermittlung einer skalaren Größe c möglichst stark zu reduzieren, kann man z. B.
die Messung k-mal wiederholen und den so erhaltenen Datenpunkten
auf die Ermittlung einer skalaren Größe c möglichst stark zu reduzieren, kann man z. B.
die Messung k-mal wiederholen und den so erhaltenen Datenpunkten
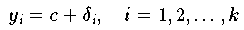
jenen Wert
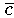 (als Schätzgröße für c) ermitteln, für den der Abstand
(als Schätzgröße für c) ermitteln, für den der Abstand
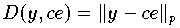 mit
mit
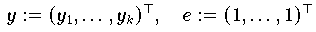
minimal wird. Für die wichtigsten Fälle der
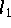 -,
-,
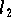 -,
-,
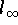 -Norm erhät man:
-Norm erhät man:
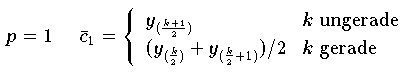
| Stichprobenmedian
|
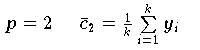
| Stichprobenmittel und
|
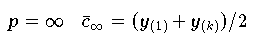
| Spannweite
|
wobei
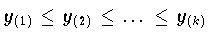 die aufsteigenden Komponenten des Vektors y bezeichnet.
die aufsteigenden Komponenten des Vektors y bezeichnet.
Für die 20 Meßwerte
99.4, 100.6, 98.4, 99.1, 101.0, 101.6, 93.8, 101.2, 99.9, 100.2
erhält man die Schätzgrößen
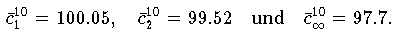
Bei näherer Betrachtung der Meßwerte erkennt man, daß der Wert 93.8 im
Vergleich zu den übrigen Werten "untypisch" klein ist. Fall die
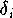 Realisierungen einer unbeschränkten (z. B. normalverteilten) Zufallsvariablen sind,
dann sind allerding beliebig kleine (und beliebig große) Werte positiver
Wahrscheinlichkeit zu erwarten. Andererseits könnte der Wert 93.8 in irgendeiner Weise verfäscht
sein (z. B. durch schlechte Meßbedingungen), so daß er als nicht repräsentativ die Größe
c und somit als "Ausreißer" anzusehen ist.
Realisierungen einer unbeschränkten (z. B. normalverteilten) Zufallsvariablen sind,
dann sind allerding beliebig kleine (und beliebig große) Werte positiver
Wahrscheinlichkeit zu erwarten. Andererseits könnte der Wert 93.8 in irgendeiner Weise verfäscht
sein (z. B. durch schlechte Meßbedingungen), so daß er als nicht repräsentativ die Größe
c und somit als "Ausreißer" anzusehen ist.
Läßt man den Wert 93.8 unberücksichtigt, dann erhält man für die restlichen 9 Beobachtungen:
![\[
\bar c_{1}^9 = 100.20, \quad
\bar c_{2}^9 = 100.16, \quad
\bar c_{\infty}^9 =100.00.
\]](pic/f04_0625.gif)
Die Änderungen der Approximationen
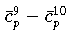 ,
,
![\[
\bar c_{1}^{9} - \bar c_{1}^{10} = 0.15, \quad
\bar c_{2}^{9} - \bar c_{2}^{10} = 0.64, \quad
\bar c_{\infty}^{9} - \bar c_{\infty}^{10} = 2.30
\]](pic/f04_0634.gif)
ist dabei für die robuste
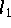 -Norm am schwächsten und für die
Maximum-Norm am stärksten.
-Norm am schwächsten und für die
Maximum-Norm am stärksten.
[ < ]
[ globale Übersicht ]
[ Kapitelübersicht ]
[ Stichwortsuche ]
[ > ]
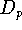 ab. Je größer p ist,
desto stärker wirken sich Ausreißer auf die Funktion g aus;
am stärksten selbstverständlich bei der Maximumnorm,
aber auch bei p = 2, bei der Euklidischen Norm,
oft immer noch unerwünscht stark.
Günstige Werte liegen etwa bei
ab. Je größer p ist,
desto stärker wirken sich Ausreißer auf die Funktion g aus;
am stärksten selbstverständlich bei der Maximumnorm,
aber auch bei p = 2, bei der Euklidischen Norm,
oft immer noch unerwünscht stark.
Günstige Werte liegen etwa bei
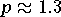 ([Ekblom [183]]).
([Ekblom [183]]).
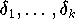 Realisierungen einer Normalverteilung mit dem Mittelwert Null sind,
dann liefert das Stichprobenmittel die optimale Schätzung für die
ungestörte Größe c,
da es unter allen linearen, erwartungstreuen Schätzfunktionen die kleinste Varianz besitzt.
Falls die Verteilungsfunktion der Störungen jedoch geringfügig von jener der Normalverteilung abweicht,
wenn z.B. eine Mischverteilung mit der Verteilungsfunktion
Realisierungen einer Normalverteilung mit dem Mittelwert Null sind,
dann liefert das Stichprobenmittel die optimale Schätzung für die
ungestörte Größe c,
da es unter allen linearen, erwartungstreuen Schätzfunktionen die kleinste Varianz besitzt.
Falls die Verteilungsfunktion der Störungen jedoch geringfügig von jener der Normalverteilung abweicht,
wenn z.B. eine Mischverteilung mit der Verteilungsfunktion
![\[
(1-\eps)\Phi + \eps H, \quad \eps \in [0,1],
\]](pic/f04_0602.gif)
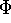 bezeichnet die Verteilungsfunktion der Normalverteilung und H
eine unbekannte Verteilungsfunktion),
dann kann mit wachsendem
bezeichnet die Verteilungsfunktion der Normalverteilung und H
eine unbekannte Verteilungsfunktion),
dann kann mit wachsendem
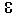 die Varianz des Stichprobenmittels
die Varianz des Stichprobenmittels
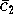 sehr schnell steigen.
sehr schnell steigen.
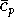 mit
mit
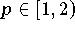 wesentlich weniger empfindlich auf Änderungen der Verteilungsfunktion reagiert.
wesentlich weniger empfindlich auf Änderungen der Verteilungsfunktion reagiert.
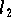 -Norm. Dabei erklärt er allenfalls,
warum viele in der Praxis auftretende Zufallsgrößen angenähert normalverteilt sind.
-Norm. Dabei erklärt er allenfalls,
warum viele in der Praxis auftretende Zufallsgrößen angenähert normalverteilt sind.
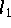 -Norm, aber auch mit
-Norm, aber auch mit
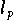 -Normen mit
-Normen mit
![$p \in (1,1.5]$](pic/f04_0609.gif) , zu robusteren,
wenngleich rechenaufwendigeren Schätzverfahren führt.
, zu robusteren,
wenngleich rechenaufwendigeren Schätzverfahren führt.
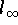 -Norm),
die zu Schätzungen führt,
die auf extreme Beobachtungen noch wesentlich empfindlicher reagiert als die entsprechenden
-Norm),
die zu Schätzungen führt,
die auf extreme Beobachtungen noch wesentlich empfindlicher reagiert als die entsprechenden
![$p \in [1,1.5]$](pic/f04_0611.gif) führen auf robuste Verfahren und sind aus diesem Grund der
führen auf robuste Verfahren und sind aus diesem Grund der
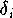 auf die Ermittlung einer skalaren Größe c möglichst stark zu reduzieren, kann man z. B.
die Messung k-mal wiederholen und den so erhaltenen Datenpunkten
auf die Ermittlung einer skalaren Größe c möglichst stark zu reduzieren, kann man z. B.
die Messung k-mal wiederholen und den so erhaltenen Datenpunkten
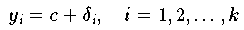
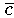 (als Schätzgröße für c) ermitteln, für den der Abstand
(als Schätzgröße für c) ermitteln, für den der Abstand
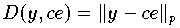 mit
mit
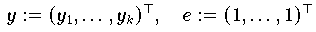
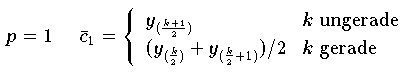
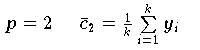
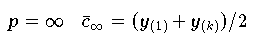
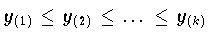 die aufsteigenden Komponenten des Vektors y bezeichnet.
die aufsteigenden Komponenten des Vektors y bezeichnet.
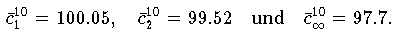
![\[
\bar c_{1}^9 = 100.20, \quad
\bar c_{2}^9 = 100.16, \quad
\bar c_{\infty}^9 =100.00.
\]](pic/f04_0625.gif)
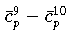 ,
,
![\[
\bar c_{1}^{9} - \bar c_{1}^{10} = 0.15, \quad
\bar c_{2}^{9} - \bar c_{2}^{10} = 0.64, \quad
\bar c_{\infty}^{9} - \bar c_{\infty}^{10} = 2.30
\]](pic/f04_0634.gif)