Computernumerik am WWW

[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]

Kondition der Polynom-Interpolation

Bei Interpolationsproblemen müssen zwei unterschiedliche Konditionsbegriffe auseinandergehalten werden:

die Kondition der Funktionswerte
und die Kondition der Koeffizienten .

Kondition der Funktionswerte

Unter der Kondition der Funktionswerte versteht man die Empfindlichkeit der Werte P_d(x) des Interpolationspolynoms gegenüber Störungen der Daten, also jener Funktionswerte, die das Polynom P_d definieren. Diese Kondition ist - im Gegensatz zur Kondition der Koeffizienten - unabhängig von der verwendeten Basis (z.B. Lagrange-, Bernstein- oder Tschebyscheff-Basis). Man untersucht in diesem Fall, wie sich der Übergang von den

$\[ \mbox{{\sl ungest$

zu den

$\[ \mbox{{\sl gest$

in einer Änderung von

$P_d(x) = \sum_{i=0}^df(x_i) \phi_{d,i}(x) \qquad \mbox{zu} \qquad \tilde{P}_d(x) = \sum_{i=0}^d\tilde{f}(x_i) \phi_{d,i}(x)$

auswirkt.

Der Interpolationsoperator

$L_d: {\cal F} \to {\P}_d$

ist jene "Vorschrift", die einer Funktion $f \in {\cal F}$ das Interpolationspolynom zu bestimmten Knoten $x_{d,0},x_{d,1},\ldots,x_{d,d}$ zuordnet:

$L_d f = \sum_{i=0}^d f(x_{d,i})\phi_{d,i}(x).$

Da es sich bei $ L_d $ um einen linearen Operator handelt, ist wegen

$\|L_d f - L_d \tilde{f}\| \le \|L_d\| \cdot \|f - \tilde{f}\|$

dessen (absolute) Kondition durch $\|L_d\|$ charakterisierbar. Die Konditionszahl

$\|L_d\| := \max \{ \|L_df\| / \|f\|: f \in {\cal F},\,f\ne0 \}$

läßt sich durch die Lebesgue-Konstante abschätzen. Aus

$\begin{eqnarray*} \|L_df\|_{\infty} & = & \max_{x \in [a,b]}|\sum_{i=0}^d f(x_{d,i})\phi_{d,i}(x)| \le \\ & \le & \max_{x \in [a,b]} \sum_{i=0}^d |f(x_{d,i})| |\phi_{d,i}(x)| \le \\ & \le & \max_{x \in [a,b]} |f(x)| \max_{x \in [a,b]} \sum_{i=0}^d |\phi_{d,i}(x)| ~ = ~ \|f\|_{\infty} \Lambda_d(K) \end{eqnarray*}$

folgt nämlich

$\|L_d\|_{\infty} \,=\, \max \{ \|L_df\|_\infty / \|f\|_\infty: f \in {\cal F}\setminus\{0\}\,\} \,\le\, \Lambda_d(K).$

Tabelle Lebesgue-Konstanten und Abb. Lebesgue-Konstanten enthalten, bezogen auf das Interpolationsintervall [-1,1] , Werte der Lebesgue-Konstante $\Lambda_d$ , die Schranken dafür darstellen, wie stark sich die Werte des Interpolationspolynoms vom Grad d maximal ändern können, wenn die Daten $f(x_{d,0}), f(x_{d,1}), \ldots, f(x_{d,d})$ mit additiven Störungen überlagert sind. Angenommen,

$\begin{array}{lcl} P_d & \quad \mbox{interpoliert} \quad & f(x_{d,0}),f(x_{d,1}),\ldots, f(x_{d,d})\quad\mbox{und} \\[.5ex] \tilde{P}_d & \quad \mbox{interpoliert} \quad & \tilde{f}(x_{d,0}), \tilde{f}(x_{d,1}),\ldots,\tilde{f}(x_{d,d}), \end{array}$

so folgt aus $|\tilde{f}(x_{d,i}) - f(x_{d,i})| \leq \delta$ , $i=0,1,\dots,d$ , die Abschätzung

$|\tilde{P}_d(x) - P_d(x)| \leq \delta \Lambda_d(K) \qquad \mbox{für alle} \quad x \in [a,b].$

Wenn z.B. $\tilde{f}(x_{d,i})$ die auf Maschinenzahlen reduzierten Funktionswerte $f(x_{d,i})$ sind, dann wird man z.B. Interpolationspolynome vom Grad 10 noch ohne Schwierigkeiten verwenden können.

Tabelle: Lebesgue-Konstanten der kubischen Spline-Interpolation (mit Not-a-knot-Randbedingungen ) und der Interpolation mit einem einzigen (,,durchgehenden``) Polynom

$\medskip \begin{table}[hbtp] \begin{footnotesize} \caption{Lebesgue-Konstanten der kubischen Spline-Interpolation (mit {\em Not-a-knot\/}-Rand\-be\-din\-gun\-gen; siehe Abschnitt~\protect\ref{ss:spline3}) und der Interpolation mit einem einzigen ($

* * *

Abbildung: Lebesgue-Konstanten
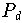$Lambda_d(K_{$ und $\Lambda_d(K_T)$ für die Interpolation mit einem Polynom P_d auf den äquidistanten Interpolationsknoten (--) bzw. den Tschebyscheff-Knoten (--) am Intervall [-1,1].

* * *

Das exponentielle Anwachsen der Lebesgue-Konstanten $\Lambda_d(K_{$ (und damit der Kondition der Polynominterpolation) bringt die Schwierigkeiten zum Ausdruck, mit denen man bei hohen Polynomgraden und äquidistanter Knotenanordnung konfrontiert ist.

Beispiel: Temperaturdaten

Die Tabelle Lebesgue-Konstanten zeigt aber auch (als Vorgriff auf Abschnitt Kubusche Spline Funktion) das vorteilhafte Verhalten der Lebesgue-Konstanten bei der Interpolation immer größer werdender Datenmengen mit kubischen Splinefunktionen. Diese sind auch bei äquidistanter Knotenanordnung und sehr großen Datenmengen ohne Schwierigkeiten verwendbar.

* * *

Kondition der Koeffizienten

Die Koeffizienten des Interpolationspolynoms 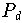P_d zu vorgegebenen Daten

$(x_0,f_0),\, (x_1,f_1),\,\dots,\,(x_d,f_d)$

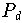lassen sich prinzipiell durch Lösung eines linearen Gleichungssystems ermitteln. Der Monombasis $\{1,x,\dots,x^d\}$ des Raumes ${\P}_d$ entspricht dabei das lineare Gleichungssystem

$\sum \limits_{j=0}^d c_j x_i^{j} = f_i, \qquad i = 0, 1, \dots, d,$

während die Basis der Tschebyscheff-Polynome auf das lineare Gleichungssystem

$\sum \limits_{j=0}^d \mbox{}'a_j T_j(x_i) = f_i, \qquad i = 0, 1, \dots, d,$

für die Koeffizienten $a_0,a_1,\ldots,a_d$ führt.

Die Matrix $(x_i^{j})$ des Gleichungssystems (1.40) ist eine Vandermondesche Matrix, die bereits für mittelgroße Polynomgrade d numerisch singulär ist, das Gleichungssystem (1.40) wird dann praktisch unlösbar. Andererseits ist die Matrix $(T_j(x_i))$ bezüglich eines speziell definierten inneren Produktes eine orthogonale Matrix - ist also optimal konditioniert - und das Gleichungssystem (1.41) ist besonders einfach zu lösen, wenn man als Interpolationsknoten $\{x_i\}$ entweder die Tschebyscheff-Nullstellen oder die Tschebyscheff-Extrema verwendet (vgl. Abschnitt Koeffizientenberechnung ).

Beispiel: Kondition der Koeffizientenberechnung

Beispiele:

Temperaturdaten

Handelt es sich bei $f(x_{11,0}), \ldots, f(x_{11,11})$ um Temperaturwerte, die man während der 12 Monate eines Jahres beobachtet hat, dann kann die Interpolation auf den äquidistanten Knoten 1, 2, ... , 12 durch ein Polynom vom Grad 11 zu unangenehmen Überraschungen führen. Die langjährigen Monatsdurchschnittswerte zeigen gute Übereinstimmung mit einem sinusförmigen Temperaturverlauf. Sie können daher durch ein Polynom vom Grad 11 relativ unproblematisch interpoliert werden.

Die Daten aus dem Jahr 1990 (vgl.\ Abb.~\ref{a1}) lagen alle im Intervall [0.6, 21.2], aber die Schwankungen im Vergleich zu den langjährigen Durchschnittswerten führen wegen der schlechten Kondition (Konditionszahl $\Lambda_{11}(K_{$ = 51.2 ) dazu, daß die Werte $P_d(x), \, x \in [1,12]$ , des Interpolationspolynoms hier im Intervall [-18, 22] liegen.

Speziell in den Randzonen zeigt sich ein "Überschwingen" des Interpolationspolynoms, das dem intuitiv erwarteten Temperaturverlauf widerspricht.

Temperaturverlauf in Wien

Abbildung: Temperaturverlauf in Wien: Monatsmittelwerte des Jahres 1990 (Datenpunkte $\bullet$ ) und durchschnittliche Monatsmittel 1951 - 1990 (Datenpunkte $\circ$ ); jeweils interpoliert durch ein Polynom vom Grad 11.

* * *

Kondition der Koeffizientenberechnung

Zur quantitativen Charakterisierung der Datenfehlerempfindlichkeit der Koeffizienten $c_0, c_1, \dots, c_d$ in (1.40) bzw. $a_0, a_1, \dots, a_d$ in (1.41) kann man die Konditionszahl

$\kappa_1(A) := \|A\|_1 \cdot \|A^{-1}\|_1$

der Matrix A := (x_i^j) bzw. A := (T_j(x_i)) heranziehen. Abb. Konditionszahlen der Koeffizientenbestimmung zeigt diese Konditionszahlen für niedrige Polynomgrade und verschiedene Kombinationen der Basiswahl und der Stützstellenanordnung (in [-1,1]):

B_M --- Monombasis $\{1,x,\dots,x^d\}$ ,
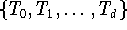B_T --- Tschebyscheff-Basis $\{T_0,T_1,\ldots,T_d\}$ ,
K_ä --- äquidistante Knoten,
K_T --- Tschebyscheff-Nullstellen als Knoten.

Abbildung: Konditionszahlen der Koeffizientenbestimmung in Abhängigkeit von Polynomgrad, Basis (Monome und Tschebyscheff-Polynome) und Knotenanordnung (äquidistant und Tschebyscheff-Nullstellen). Man beachte den logarithmischen Maßstab auf der Ordinate!

[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]

	die Kondition der Funktionswerte
und	die Kondition der Koeffizienten .

B_M	---	Monombasis $\{1,x,\dots,x^d\}$ ,
B_T	---	Tschebyscheff-Basis $\{T_0,T_1,\ldots,T_d\}$ ,
K_ä	---	äquidistante Knoten,
K_T	---	Tschebyscheff-Nullstellen als Knoten.