[ < ]
[ globale Übersicht ]
[ Kapitelübersicht ]
[ Stichwortsuche ]
[ > ]
Wenn man eine Funktion f auf
einem Intervall [a,b] durch ein Interpolationspolynom
approximieren will und über die Interpolationsknoten frei verfügen kann,
dann sollte man unbedingt die Tschebyscheff-Abszissen verwenden.
Man hat dann gegenüber äquidistanten Knoten folgende Vorteile:
-
Wegen Ungleichung
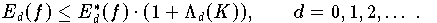 Formel 7.7.2
Formel 7.7.2
(Siehe Satz)
ist auch für sehr hohe Grade das so erhaltene Interpolationspolynom
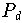 in seiner Approximationsqualität kaum schlechter als das bezüglich der
Maximumnorm bestapproximierende Polynom
in seiner Approximationsqualität kaum schlechter als das bezüglich der
Maximumnorm bestapproximierende Polynom
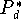 .
.
-
Die Empfindlichkeit gegenüber Datenstörungen
(die Kondition des Interpolationsproblems)
ist schon ab mittleren Polynomgraden deutlich geringer
als bei Verwendung äquidistanter Interpolationsknoten.
-
Die Berechnung einer Tschebyscheff-Darstellung von
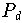 ist sehr effizient durch Auswertung von (
ist sehr effizient durch Auswertung von (
 )
bzw. (
)
bzw. (
 )
möglich.
)
möglich.
Wenn man sich für die Funktionsapproximation durch Interpolation an
den Tschebyscheff-Knoten entschieden hat,
bleibt noch die Frage nach der Wahl der Anzahl der Interpolationsknoten
und damit verbunden des Polynomgrades d .
Soferne man über Abschätzungen der Ableitungen von f verfügt,
kann man die Fehlerformel (
 )
anwenden. Für
)
anwenden. Für
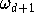 gilt
gilt

Da die
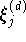 laut Voraussetzung die Nullstellen des Tschebyscheff-Polynoms
laut Voraussetzung die Nullstellen des Tschebyscheff-Polynoms
 sind, ist
sind, ist
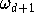 in diesem Fall ein Vielfaches von
in diesem Fall ein Vielfaches von
 . Aus der
. Aus der
und weiters, daß die Tschebyscheff-Abszissen jene Interpolationsknoten in
[-1,1] sind, für die
![\max \{ |\omega_{d+1}(x)|: x \in [-1,1] \}]( pic/f07_0907.gif )
minimal ist,
was neuerlich die Sonderstellung der Tschebyscheff-Abszissen betont.
Die Abschätzung (
 )
für den Interpolationsfehler lautet daher in diesem Spezialfall
)
für den Interpolationsfehler lautet daher in diesem Spezialfall
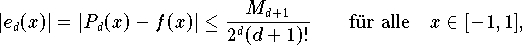 ,
,
wobei
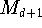 eine Schranke für den Betrag der Ableitung
eine Schranke für den Betrag der Ableitung
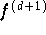 auf [-1,1] bezeichnet.
auf [-1,1] bezeichnet.
Das Beispiel
Approximation der Sinusfunktion
zeigt die Anwendung des Gelernten.
Eine Alternative zum
Abbruch der Entwicklung eines Interpolationspolynoms
mit zu hohem Grad
besteht im
sukzessiven Erhöhen des Polynomgrades
, bis man die gewünschte Approximationsgenauigkeit erreicht hat.
Die beiden Vorgehensweisen werden nun genauer beläuchtet.
* * *
Im häufig auftretenden Fall, daß man über die Ableitungen von f
keine Information besitzt, kann man die Polynominterpolation an den
Tschebyscheff-Knoten auf folgende Art einsetzen:
Man wählt eine Stützstellenanzahl, bei der mit großer Wahrscheinlichkeit der
benötigte Polynomgrad (bei dem man die geforderte Genauigkeit erreicht)
überschritten wird. Dann benützt man folgende Eigenschaft der
Koeffizienten
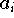 der Entwicklung
der Entwicklung
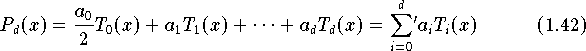
des Interpolationspolynoms
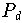 . Die Beträge
. Die Beträge
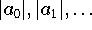 fallen bis zu einem Niveau,
das durch die Genauigkeit der Funktionswerte bestimmt wird
(dies kann auch die Genauigkeit der Maschinenzahlen
fallen bis zu einem Niveau,
das durch die Genauigkeit der Funktionswerte bestimmt wird
(dies kann auch die Genauigkeit der Maschinenzahlen
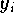 sein, falls sonst keine Störungen der Funktionswerte vorliegen).
sein, falls sonst keine Störungen der Funktionswerte vorliegen).


Bei dieser Vorgangsweise verwendet man aber nicht die
Nullstellen, sondern die Extremstellen der Tschebyscheff-Polynome als
Interpolationsknoten. Man kommt auf diese Art zu Interpolationspolynomen mit
fast gleich guten Approximationseigenschaften, die den Vorteil haben, daß
beim Übergang vom Polynom
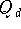 zum Polynom
zum Polynom
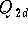 sämtliche
f-Auswertungen, die man für die Bestimmung von
sämtliche
f-Auswertungen, die man für die Bestimmung von
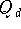 benötigt, bei der Berechnung von
benötigt, bei der Berechnung von
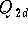 wieder verwendet werden können. Man kann dann z.B.
wieder verwendet werden können. Man kann dann z.B.
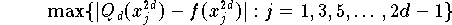
als Fehlerschätzung verwenden,
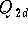 berechnen und gegebenenfalls die Entwicklung abbrechen.
berechnen und gegebenenfalls die Entwicklung abbrechen.
* * *
Beispiele:
Approximation der Sinusfunktion
Die Implementierung der trigonometrischen Funktionen als vordefinierte
Unterprogramme in den höheren Programmiersprachen
erfolgt oft mit approximierenden Polynomen in
einem Periodenintervall oder einem Teil davon. Approximiert man z.B.
sin (x) durch ein Interpolationspolynom
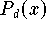 an den
Tschebyscheff-Knoten im Intervall
an den
Tschebyscheff-Knoten im Intervall
![[-\pi/2,\pi/2]](pic/f07_0922.gif) , so ergibt sich wegen
, so ergibt sich wegen
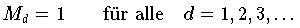
und
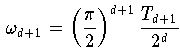 ,
,
wobei der Faktor
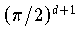 von der Umskalierung von [-1,1]
auf
von der Umskalierung von [-1,1]
auf
![[-\pi/2,\pi/2]](pic/f07_0922.gif) herrührt, die Fehlerabschätzung
herrührt, die Fehlerabschätzung
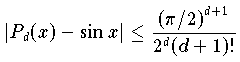
Das Polynom
P9
mit einer Fehlerschranke
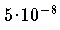 würde für
würde für
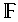 (2,24,-125,128,true) bereits eine
zufriedenstellende absolute Approximationsgenauigkeit liefern.
Durch Verkleinerung des Interpolationsintervalls auf
(2,24,-125,128,true) bereits eine
zufriedenstellende absolute Approximationsgenauigkeit liefern.
Durch Verkleinerung des Interpolationsintervalls auf
![[0,\pi/4]](pic/f07_0928.gif) und gleichzeitige Approximation von cos (x) kann der erforderliche
Polynomgrad d noch weiter gesenkt werden.
und gleichzeitige Approximation von cos (x) kann der erforderliche
Polynomgrad d noch weiter gesenkt werden.
* * *
Approximation der Exponentialfunktion
Interpoliert man
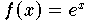 auf dem Intervall
auf dem Intervall
![\left[-\frac{\ln 2}{2},\,\frac{\ln 2}{2}\right]\,\approx\,\left[-0.347,\, 0.347\right]](pic/f07_0930.gif)
an den Tschebyscheff-Nullstellen durch
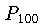 , dann zeigen die Beträge
, dann zeigen die Beträge
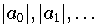 das aus Tabelle~\ref{tab:09.KO} ersichtliche
Abklingverhalten.
das aus Tabelle~\ref{tab:09.KO} ersichtliche
Abklingverhalten.
![\begin{table}[hbtp]
\caption{Koeffizienten der Entwicklung (\protect\ref{eqn:09.KO}) für die
Exponentialfunktion}
\label{tab:09.KO}
\begin{center}
\begin{tabular}{||c|l||c|l||}
\hline
\strutHline
$i$ & \multicolumn{1}{c||}{$|a_i|$} & $i$ & \multicolumn{1}{c||}
{$|a_i|$} \\
\hline
\strutNachHline
0 & $ 2.532 $ & 5 & $ 5.429 \cdot 10^{-4}$ \\
1 & $ 1.130 $ & 6 & $ 4.498 \cdot 10^{-5}$ \\
2 & $ 2.715 \cdot 10^{-1}$ & 7 & $ 3.049 \cdot 10^{-6}$ \\
3 & $ 4.434 \cdot 10^{-2}$ & 8 & $ 4.528 \cdot 10^{-7}$ \\
\strutVorHline
4 & $ 5.474 \cdot 10^{-3}$ & 9 & $ 3.294 \cdot 10^{-7}$ \\
\hline
\end{tabular}
\end{center}
\end{table}](pic/f07_0931.gif)
Die Werte
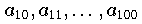 bleiben bei einfach genauer Rechnung alle in der Größenordnung
bleiben bei einfach genauer Rechnung alle in der Größenordnung
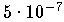 . Man wird in diesem Fall die abgebrochene Entwicklung
. Man wird in diesem Fall die abgebrochene Entwicklung
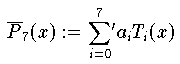
mit 8 Koeffizienten als Approximation verwenden. Das schnelle Abfallen
der
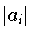 gegen den "Minimalpegel" ist bei glatten Funktionen, wie bei
diesem Beispiel, besonders deutlich. Das Polynom
gegen den "Minimalpegel" ist bei glatten Funktionen, wie bei
diesem Beispiel, besonders deutlich. Das Polynom
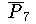 stellt das bestapproximierende Polynom im Sinne der kleinsten Quadrate dar
(siehe Abschnitt~\ref{s:l2approx}).
stellt das bestapproximierende Polynom im Sinne der kleinsten Quadrate dar
(siehe Abschnitt~\ref{s:l2approx}).
* * *
Approximation der Logarithmusfunktion
Interpoliert man
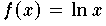 auf dem Intervall [0.71,1.41] an 100
Tschebyscheff-Nullstellen, verwendet aber nur k=1,2,...,30 Koeffizienten,
so nimmt das Maximum des Approximationsfehlers den nachfolgend dargestellten Verlauf.
auf dem Intervall [0.71,1.41] an 100
Tschebyscheff-Nullstellen, verwendet aber nur k=1,2,...,30 Koeffizienten,
so nimmt das Maximum des Approximationsfehlers den nachfolgend dargestellten Verlauf.

Abbildung: Maximaler absoluter Fehler bei abgebrochener
Tschebyscheff-Interpolation der Logarithmusfunktion zu 100
Knoten im Intervall
![[1/\protect\sqrt{2},\protect\sqrt{2}] \approx[0.71,1.41]](pic/f07_0940.gif)
Bereits mit 10 Koeffizienten ist das Maximum
des absoluten Approximationsfehlers auf
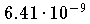 abgesunken (siehe die nachfolgende Abbildung).
abgesunken (siehe die nachfolgende Abbildung).

Abbildung: Absoluter Fehler der nach 10 Koeffizienten abgebrochenen
Tschebyscheff-Interpolation der Logarithmusfunktion zu 100
Knoten im Intervall
![[1/\protect\sqrt{2},\protect\sqrt{2}] \approx[0.71,1.41]](pic/f07_0940.gif)
[ < ]
[ globale Übersicht ]
[ Kapitelübersicht ]
[ Stichwortsuche ]
[ > ]
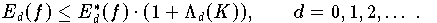 Formel 7.7.2
Formel 7.7.2
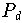 in seiner Approximationsqualität kaum schlechter als das bezüglich der
Maximumnorm bestapproximierende Polynom
in seiner Approximationsqualität kaum schlechter als das bezüglich der
Maximumnorm bestapproximierende Polynom
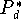 .
.
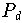 ist sehr effizient durch Auswertung von (
ist sehr effizient durch Auswertung von (
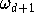 gilt
gilt

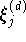 laut Voraussetzung die Nullstellen des Tschebyscheff-Polynoms
laut Voraussetzung die Nullstellen des Tschebyscheff-Polynoms
 sind, ist
sind, ist
![\max \{ |\omega_{d+1}(x)|: x \in [-1,1] \}]( pic/f07_0907.gif )
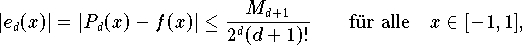 ,
,
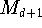 eine Schranke für den Betrag der Ableitung
eine Schranke für den Betrag der Ableitung
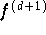 auf [-1,1] bezeichnet.
auf [-1,1] bezeichnet.
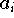 der Entwicklung
der Entwicklung
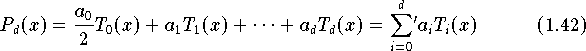
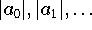 fallen bis zu einem Niveau,
das durch die Genauigkeit der Funktionswerte bestimmt wird
(dies kann auch die Genauigkeit der Maschinenzahlen
fallen bis zu einem Niveau,
das durch die Genauigkeit der Funktionswerte bestimmt wird
(dies kann auch die Genauigkeit der Maschinenzahlen
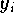 sein, falls sonst keine Störungen der Funktionswerte vorliegen).
sein, falls sonst keine Störungen der Funktionswerte vorliegen).


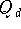 zum Polynom
zum Polynom
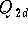 sämtliche
f-Auswertungen, die man für die Bestimmung von
sämtliche
f-Auswertungen, die man für die Bestimmung von
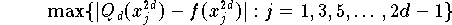
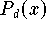 an den
Tschebyscheff-Knoten im Intervall
an den
Tschebyscheff-Knoten im Intervall
![[-\pi/2,\pi/2]](pic/f07_0922.gif) , so ergibt sich wegen
, so ergibt sich wegen
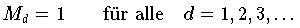
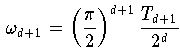 ,
,
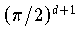 von der Umskalierung von [-1,1]
auf
von der Umskalierung von [-1,1]
auf
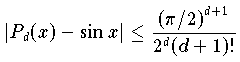
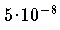 würde für
würde für
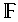 (2,24,-125,128,true) bereits eine
zufriedenstellende absolute Approximationsgenauigkeit liefern.
Durch Verkleinerung des Interpolationsintervalls auf
(2,24,-125,128,true) bereits eine
zufriedenstellende absolute Approximationsgenauigkeit liefern.
Durch Verkleinerung des Interpolationsintervalls auf
![[0,\pi/4]](pic/f07_0928.gif) und gleichzeitige Approximation von cos (x) kann der erforderliche
Polynomgrad d noch weiter gesenkt werden.
und gleichzeitige Approximation von cos (x) kann der erforderliche
Polynomgrad d noch weiter gesenkt werden.
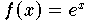 auf dem Intervall
auf dem Intervall
![\left[-\frac{\ln 2}{2},\,\frac{\ln 2}{2}\right]\,\approx\,\left[-0.347,\, 0.347\right]](pic/f07_0930.gif)
 , dann zeigen die Beträge
, dann zeigen die Beträge
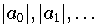 das aus Tabelle~\ref{tab:09.KO} ersichtliche
Abklingverhalten.
das aus Tabelle~\ref{tab:09.KO} ersichtliche
Abklingverhalten.
![\begin{table}[hbtp]
\caption{Koeffizienten der Entwicklung (\protect\ref{eqn:09.KO}) für die
Exponentialfunktion}
\label{tab:09.KO}
\begin{center}
\begin{tabular}{||c|l||c|l||}
\hline
\strutHline
$i$ & \multicolumn{1}{c||}{$|a_i|$} & $i$ & \multicolumn{1}{c||}
{$|a_i|$} \\
\hline
\strutNachHline
0 & $ 2.532 $ & 5 & $ 5.429 \cdot 10^{-4}$ \\
1 & $ 1.130 $ & 6 & $ 4.498 \cdot 10^{-5}$ \\
2 & $ 2.715 \cdot 10^{-1}$ & 7 & $ 3.049 \cdot 10^{-6}$ \\
3 & $ 4.434 \cdot 10^{-2}$ & 8 & $ 4.528 \cdot 10^{-7}$ \\
\strutVorHline
4 & $ 5.474 \cdot 10^{-3}$ & 9 & $ 3.294 \cdot 10^{-7}$ \\
\hline
\end{tabular}
\end{center}
\end{table}](pic/f07_0931.gif)
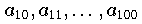 bleiben bei einfach genauer Rechnung alle in der Größenordnung
bleiben bei einfach genauer Rechnung alle in der Größenordnung
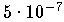 . Man wird in diesem Fall die abgebrochene Entwicklung
. Man wird in diesem Fall die abgebrochene Entwicklung
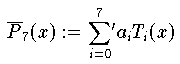
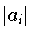 gegen den "Minimalpegel" ist bei glatten Funktionen, wie bei
diesem Beispiel, besonders deutlich. Das Polynom
gegen den "Minimalpegel" ist bei glatten Funktionen, wie bei
diesem Beispiel, besonders deutlich. Das Polynom
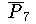 stellt das bestapproximierende Polynom im Sinne der kleinsten Quadrate dar
(siehe Abschnitt~\ref{s:l2approx}).
stellt das bestapproximierende Polynom im Sinne der kleinsten Quadrate dar
(siehe Abschnitt~\ref{s:l2approx}).
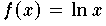 auf dem Intervall [0.71,1.41] an 100
Tschebyscheff-Nullstellen, verwendet aber nur k=1,2,...,30 Koeffizienten,
so nimmt das Maximum des Approximationsfehlers den nachfolgend dargestellten Verlauf.
auf dem Intervall [0.71,1.41] an 100
Tschebyscheff-Nullstellen, verwendet aber nur k=1,2,...,30 Koeffizienten,
so nimmt das Maximum des Approximationsfehlers den nachfolgend dargestellten Verlauf.

![[1/\protect\sqrt{2},\protect\sqrt{2}] \approx[0.71,1.41]](pic/f07_0940.gif)
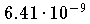 abgesunken (siehe die nachfolgende Abbildung).
abgesunken (siehe die nachfolgende Abbildung).
