Computernumerik am WWW

[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]

6.7.7 Konvergenz der Interpolationspolynome

Satz (Weierstraß)
Knotenmatrizen
Lebesgue-Funktionen und -Konstanten
Konvergenz bezüglich der Tschebyscheff-Knoten
Konvergenz bezüglich äquidistanter Knoten
Beispiele

6.7.7 Konvergenz der Interpolationspolynome

Es erhebt sich die Frage, ob die Vorgangsweise des globalen Erhöhens der Parameteranzahl der Approximationsfunktion (P_d $\in$ $\P$ _d und $d \to \infty$ ) stets zum Ziel führt, wenn man z.B. annimmt, daß f auf [a,b] stetig ist. Der folgende Satz von K. Weierstraß (1885) scheint die Bejahung dieser Frage nahezulegen:

Satz (Weierstraß)

Für jede Funktion f $\in$ C[a , b] gibt es zu jedem beliebigen $\eps > 0$ > 0 ein Polynom P $\in$ $\P$ , das

$|P(x) - f(x)| \leq \eps \qquad \mbox{f$
erfüllt.
Von K.Weierstraß selbst stammen nur nicht-konstruktive Beweise seines Approximationssatzes. Der erste konstruktive Beweis geht auf S.N.Bernstein (1912) zurück. Dabei wird gezeigt, daß die mit Hilfe der Bernstein-Polynome {b_d,i} konstruierte Folge von Polynomen

$P_d(x;f) := \sum_{i=0}^d f(i/d) b_{d,i} = \sum \limits_{i=0}^d f(i/d) {d \choose i} x^i (1-x)^{d-i}, \quad d =1,2,3,\dots\,,$ Formel (7.7.1)

auf [0,1] gleichmäßig gegen f konvergiert. Eine detaillierte Darstellung dieses Beweises findet man z.B. bei Davis[38].
Für die praktische Lösung von Approximationsproblemen sind die durch (7.7.1) definierten Polynome wegen ihrer extrem langsamen Konvergenz nicht geeignet (siehe Abbildung 7.7.1). Bemerkenswert ist hingegen die gute Wiedergabe der Formeigenschaften von f (Anzahl und Lage der Extremwerte, Wendepunkte etc.) durch die Polynome P_d(x;f). Sie werden deshalb auch für Anwendungen in der Graphischen Datenverarbeitung herangezogen.
Auch der konstruktive Beweis des Satzes von Weierstraß liefert somit keinen praktischen brauchbaren Weg, wie man in einer konkreten Situation (d.h. bei gegebenem f und $\varepsilon$ ) zu einem Polynom einer vorgegebenen Approximationsgüte kommen kann.

Abbildung 7.7.1: Approximation der Runge-Funktion f(x) := (1+25x²)^-1 durch die PolynomeP_d(x;f), d=4,8,12,16. Beachtenswert ist die extrem geringe Konvergenzgeschwindigkeit.

Knotenmatrizen

Im Gegensatz zur Bestapproximation, wo der algorithmische Aufwand zur Bestimmung einer Approximationsfunktion sehr stark von der zu approximierenden Funktion abhängt, kann man beim Interpolationsprinzip eine sehr starke algorithmische Vereinfachung erreichen, wenn man die Folge der Interpolationsknoten {x_d,0, x_d,1, ...., x_d,d}, d=0,1,2,..., a priori festlegt.
Durch die Nicht-Adaptivität der resultierenden Algorithmen kann man z.B. spezielle Rechnerstrukturen - vor allem Parallelrechner - besser ausnutzen und eine vollständige oder weitgehende Wiederverwendung bereits vorliegender Auswertungen der zu approximierenden Funktion f(x_d,i) in den darauffolgenden Schritten d+1, d+2, ... sicherstellen.

Definition (Knotenmatrix)

Das a priori (unabhängig von den approximierenden Funktionen) festgelegte Stützstellenschema einer unendlichen Folge {P₀, P₁, P₂,...} von Interpolationspolynomen

$K = \left( \begin{array}{llll} x_{0,0} & & & \\ x_{1,0} & x_{1,1} & & \\ x_{2,0} & x_{2,1} & x_{2,2} & \\ \vdots & \vdots & \vdots & \ddots \end{array} \right)$
nennt man Knotenmatrix.

Die Wahl einer universellen, vom konkreten Approximationsproblem unabhängigen Knotenmatrix beeinflußt in sehr starkem Maß die Eigenschaften eines darauf aufbauenden (nicht-adaptiven) Interpolationsalgorithmus. Je umfassender z.B. die Menge jener Funktionen ist, bei der die Konvergenz der Interpolationspolynome mit $d \to \infty$ sichergestellt ist, desto größer ist der Anwendungsbereich des entsprechenden Interpolationsalgorithmus. Die Konvergenz garantiert nämlich für jede geforderte Approximationsgenauigkeit r>0, daß der Interpolationsalgorithmus, der auf einem sukzessiven Berechnen der Polynome zu den Knoten {x_d,0, x_d,1, ...., x_d,d}, d=0,1,2,.., beruht, nach endlich vielen Schritten erfolgreich abgebrochen werden kann (wobei Fragen des Rechenaufwandes und der Rundungsfehlereinflüsse zunächst nicht in Betracht gezogen werden). Nach dem Satz von Weierstraß könnte man vermuten, daß die Funktionenklassen, für die Konvergenz garantiert werden kann, alle stetigen Funktionen f $\in$ C[a,b] umfaßt. Diese naheliegende Vermutung ist jedoch falsch, wie der folgende Satz zeigt.

Satz (Faber)
Es existiert keine universelle Knotenmatrix K, mit der die zugehörigen Interpolationspolynome für jede Funktion f $\in$ C[a,b] gegen f konvergieren.

Die Aussage des Satzes von Faber steht nicht im Widerspruch zum Satz von Weierstraß, da man für jede einzelne Funktion f $\in$ C[a,b] durchaus eine Knotenmatrix K angeben kann, für die P_j(f) gegen f gilt. Man muß dazu nur die in [a,b] gelegenen Nullstellen der Fehlerfunktion der bezüglich der Maximumnorm bestapproximierenden Polynome P₀^*, P₁^*, P₂^*,... in K zusammenfassen.

Lebesgue-Funktionen und -Konstanten

Wenn man die auf definierte Funktionenklasse F gegenüber C[a,b] verkleinert, so gelingt es, universelle Knotenmatrizen zu finden, bei denen die Konvergenz für jede Funktion f $\in$ F gilt. Für die erforderlichen Konvergenzuntersuchungen werden die wichtigen Begriffe des Lebesgue-Funktionen und die -Konstanten benötigt.

Definition (Lebesgue-Funktion)
Die Betragssumme der Lagrange Polynome zu den Knoten x_d,0, x_d,1, ...., x_d,d der Knotenmatrix K

$\lambda_d(x;K) := \sum \limits_{i=0}^d | \varphi_{d,i}(x)|$
heißt Lebesgue-Funktion der Ordnung d+1 von K (siehe Abb. 7.7.2 und 7.7.3).

Lebesgue-Funktion (sechs Tschebyscheff-Knoten; sechs &aumlquidistanten Knoten)

Abb. 7.7.2: Lebesgue-Funktion

₅ der Polynominterpolation zu den sechs Tschebyscheff-Knoten und den sechs äquidistanten Knoten auf [-1,1]

Lebesgue-Funktion (12 Tschebyscheff-Knoten; 12 &aumlquidistanten Knoten)

Abb. 7.7.3: Lebesgue-Funktion

₁₁ der Polynominterpolation zu den 12 Tschebyscheff-Knoten und den 12 äquidistanten Knoten auf [-1,1]

Definition (Lebesgue-Konstante)
Die Größe

$\Lambda_d(K) := \max \{ \lambda_d(x;K): x \in [a,b] \}$
heißt Lebesgue-Konstante der Ordnung d+1 von K (bezüglich des Intervalls[a,b]).

Mit Hilfe der Lebesgue-Konstante kann ein Zusammenhang zwischen dem Fehler der Interpolationspolynome {P_d(f)} bezüglich einer Knotenmatrix K und dem jeweils optimalen (kleinstmöglichen) Approximationsfehler aller Polynome vom Grad d hergestellt werden.

Die Approximationsqualität einer Folge interpolierender Polynome {P_d} (die durch eine Knotenmatrix K definiert ist) bezüglich einer Funktion f ist durch den jeweils maximalen Interpolationsfehler

$E_d := E_d(f) := \| e_d \|_{\infty} = \max \limits_{x \in [a,b]} |P_d(x) - f(x)|, \qquad d=0,1,2,\dots\,,$
charakterisiert. Die Größen E_d sind umso günstiger, je näher sie bei den jeweils kleinstmöglichen Zahlen

$E_d^{*} := E_d^{*}(f) := \min \{ \|P_d - f \|_{\infty} : P_d \in \P_d \} = \| P_d^{*} - f \|_{\infty}$
liegen, die man für die bestapproximierenden Polynome P_d vom Grad d erhält.

Satz
Für eine Funktion f $\in$ C[a,b] und eine Folge von Interpolationsprolynomen (P_d(f))bezüglich der Knotenmatrix K gilt:

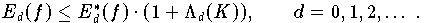$E_d(f) \leq E_d^{*}(f) \cdot (1 + \Lambda_d(K)),\qquad d = 0,1,2,\dots\,.$ Formel 7.7.2
Beweis: Rivlin (341).

Die Lebesgue-Konstanten , die zwar von der universellen Knotenmatrix K abhängen, aber von f unabhängig sind, bilden also ein Maß dafür, wie stark der Interpolationsfehler E_d den optimalen Wert (die untere Schranke) E_d ungünstigstenfalls überschreiten kann. Je kleiner die Lebesgue-Konstanten einer Knotenmatrix sind, desto näher wird der maximale Interpolationsfehler dem kleinstmöglichen Approximationsfehler sein.
Nach dem Satz von Faber kann die Folge {}, die von f unabhängig ist, nicht beschränkt sein, es muß gegen unendlich gelten. Erdös [187] hat gezeigt, daß es für jede Knotenmatrix K eine Konstante c > 0 gibt, mit der gilt:

$\Lambda_d(K) > \frac{2}{\pi} \ln d - c, \qquad ~d=1,2,\ldots\ .$

Die Knotenmatrix K als definierender Bestandteil von nicht-adaptiven Approximationsalgorithmen auf Interpolationsbasis kann - durch ihren Einfluß auf die Konvergenzgeschwindigkeit - die Effizienz der entsprechenden Algorithmen wesentlich bestimmen. Je näher (K) an der nicht zu unterschreitenden Schranke liegt, desto effizienter wird der auf K aufbauende Algorithmus sein. Falls (K) wesentlich rascher wächst als die untere Schranke, so grenzt dies unter Umständen die Klasse jener Funktionen, für die Konvergenz garantiert werden kann, eng ein.
Die Existenz der "idealen" Knotenmatrix , die für alle Polynomgrade die kleinstmögliche Lebesgue-Konstante liefert, ist zwar theoretisch gesichert (de Boor, Pinnkus [156]), die Matrix ist aber (noch) nicht bekannt. Eine nicht optimale, aber sehr günstige Folge von Interpolationsknoten ist durch die Nullstellen (9.16) der Tschebyscheff-Polynome gegeben.

Die Knotenmatrix ist auf das Interpolationsintervall [-1,1] bezogen. Ein anderes Intervall [a,b] kann durch eine affine Transformation der unabhängigen Veränderlichen auf [-1,19] gebracht werden:

$\overline{x} := \frac{2x - b - a}{b - a}.$
Daß es sich bei der K_T um eine nahezu optimale Wahl von universellen Interpolationsknoten handelt, zeigt der folgende Satz:

Satz 9.3.7
Die Lebesgue-Konstanten von K_T erfüllen die Ungleichung

$\frac{2}{\pi} \ln d + 0.9625 < \Lambda_d(K_T) \leq \frac{2}{\pi} \ln d + 1,\qquad d = 1,2,\ldots\,.$ Formel (7.7.3)
Beweis: Rivlin (341).

Selbst für den hohen Polynomgrad d=1000 gilt erst

$E_{1000}(f) \le 6.4 \cdot E_{1000}^{*}(f).$
Das Interpolationspolynom vom Grad d = 1000 zu den Tschebyscheff-Knoten besitzt einen Approximationsfehler, der selbst im ungünstigsten Falle nur 6.4-mal so groß ist wie der optimale Approximationsfehler E₁₀₀₀^*.

Konvergenz bezüglich der Tschebyscheff-Knoten

Für $d \to \infty$ gilt nach dem Satz von Weierstraß für jede Funktion aus C[a,b]. Wie von Erdös und Vertesi (188) gezeigt wurde, gibt es für jede Knotenmatrix - also auch für die Tschebyscheff-Knoten - eine Funktion f $\in$ C[a,b], für die die Folge der Interpolationspolynome auf dem ganzen Intervall [a,b] divergiert (mit Ausnahme eventuell endlich vieler Punkte). Schränkt man die Funktionenklasse aber etwas ein, z.B. auf jene Funktionen, die auf [-1,1] Lipschitz-stetig sind, d.h. auf Funktionen, die für eine Konstante L - die sogenannte Lipschitz-Konstante - die Ungleichung

$|f(u) - f(v)| \leq L|u - v| \qquad \mbox{f$
erfüllen, so liefert der folgende Satz die Grundlage, um Konvergenz in allen Fällen nachweisen zu können.

Satz (Jackson)
Für alle auf [-1,1] Lipschitz-stetigen Funktionen mit der Lipschitz- Konstante L gilt die Fehlerschranke

$E_d^{*}(f) \,\leq\, \frac{L}{2d + 2}.$ Formel (7.7.4)
Beweis: Cheney (35).

Für die Knotenmatrix K_T erhält man durch Kombination von (7.7.2), (7.7.3) und (7.7.4) eine obere Schranke für den Approximationsfehler der Interpolationspolynome {P_d}, die für $d \to \infty$ gegen 0 strebt:

$E_d(f) \,\leq\, E_d^{*}(f) \cdot (1 + \Lambda_d) \,\leq\, \frac{L }{2d + 2} \left(\frac{2}{\pi} \ln d + 2\right).$
Für jede Lipschitz-stetige Funktion f gibt es somit zu jeder Toleranz r einen Polynomgrad d, für den das auf den Tschebyscheff-Nullstellen interpolierende Polynom P_d(f) eine maximale Abweichung r von f hat. Die Menge der Funktionen, für die ein auf K_T operierender Interpolationsalgorithmus (ohne Berücksichtigung von Rechenaufwands- und Genauigkeits- Restriktionen) konvergiert, umfaßt daher alle Lipschitz-stetigen, nicht aber alle stetigen Funktionen.

In der Praxis sind viele wichtigen Funktionen einmal oder öfter stetig differenzierbar. Für diese Funktionen ist bei Verwendung der Tschebyscheff-Knoten K_T die Konvergenz auf jeden Fall sichergestellt.
Ähnlich günstige Eigenschaften wie die Knotenmatrix der Tschebyscheff-Nullstellen besitzt die Knotenmatrix der Tschebyscheff-Extrema (9.17).
Interpoliert man unstetige Funktionen mit Sprungstellen durch Polynome zu den Tschebyscheff- Knoten K_T, so tritt ein Überschwingen auf, dessen Maximal- und Minimalamplitude vom Polynomgrad d (nahezu) unabhängig ist. Diese Besonderheit, die auch bei den Teilsummen von Fourier- Reihen in der Nähe von Sprungstellen auftritt, heißt Gibbsches Phänomen .

Konvergenz bezüglich äquidistanter Knoten

Eine Knotenverteilung, die - vor allem aus algorithmischen Gründen - wesentlich naheliegender ist als jene der Tschebyscheff-Knoten, ist die äquidistante Verteilung

$x_{d,j} = \frac{2j}{d} - 1, \qquad j = 0, 1, \dots, d, \qquad d = 1,2,3,\ldots\,.$
Auch im äquidistanten Fall wird, um die Vergleichbarkeit herzustellen, die Knotenmatrix K_ä = (x_d,j) auf [-1,1] bezogen.
Im Gegensatz zur K_T und K_U, wo die Lebesgue-Konstanten mit steigendem Polynomgrad logarithmisch gegen $\infty$ streben, wachsen bei äquidistanter Knotenverteilung die Lebesgue-Konstanten jedoch exponentiell. Bei äquidistanten Knoten ist selbst die k-malige Differenzierbarkeit von f nicht hinreichend für die Konvergenz der Interpolationspolynome . Nicht einmal bei beliebig (unendlich) oft differenzierbaren Funktionen ist die Konvergenz garantiert.

Erst unter der außerordentlich einschränkenden Annahme, daß sich $\to\R$ zu einer ganzen Funktion : $\to\C$ fortsetzen läßt, sodaß die Potenzreihendarstellung von $\hat f$ in der gesamten komplexen Ebene $\C$ konvergiert, ist die Konvergenz auf äquidistanten Interpolationsknoten sichergestellt(Hämmerlin,Hoffmann [50]).
Die Eigenschaft der Interpolationspolynome auf äquidistanten Knoten , bei vielen "harmlosen", im mathematischen Sinn "sehr glatten" Funktionen für $d \to \infty$ nicht zu konvergieren, macht sich bereits bei niederen Polynomgraden durch ein starkes Oszillieren des Interpolationspolynoms bemerkbar (siehe Abb 7.7.4).

Polynom-Interpolation der Runge-Funktion auf &aumlquidistanten Knoten

Abbildung 7.7.4: Polynom-Interpolation der Runge-Funktion auf äquidistanten Knoten

Ein Nachteil der Interpolation mit äquidistanten Knoten ist auch deren schlechte Kondition, das empfindliche Reagieren der Werte P_d(x) des Interpolationspolynoms auf Änderungen der Daten {f(x₀),....,f(x_d)} (siehe Abschnitt 7.8).
Die Interpolation mit einem Polynom auf gleichabständigen Knoten ist somit nur für relativ kleine Polynomgrade praktisch brauchbar. Ist die Verwendung äquidistanter Interpolationsknoten aus irgendeinem Grund erforderlich oder erwünscht, so kommt bei einer größeren Anzahl von Datenpunkten nur eine stückweise aus Polynomen niedrigerer Grade zusammengesetzte Funktion in Betracht (siehe Abschnitt 9.4).

Beispiele

Beispiel (Rampenfunktion)
Interpoliert man die Lipschitz-stetigen (aber nicht differenzierbare) Funktion

$f(x):=\left\{ \begin{array}{ll} 0 & \mbox{f$ Formel (7.7.5)
durch Polynome Pd zu den auf (0,1) transformierten Tschebyscheff-Abszissen, so konvergiert

$P_d(x)\to f(x)\qquad\mbox{f$
Für 40 Knotenpunkte erhält man den in Abb 7.7.5 dargestellten Funktionsverlauf.

Abb. 7.7.5: Funktion (7.7.5) interpoliert durch ein Polynom zu 40 Tschebyscheff-Abszissen.

Beispiel (Sprungfunktion)
Interpoliert man die unstetige Sprungfunktion

$f(x):=\left\{ \begin{array}{ll} 0 & \mbox{f$ Formel (7.7.6)
durch Polynome P_d zu den auf [0,1] transformierten Tschebyscheff-Abszissen, so konvergiert mit Ausnahme der Sprungstelle x = 0.6 (siehe Abb 7.7.6, Abb 7.7.7 und Abb 7.7.8). In der Nähe der Spungstelle ist in den Abbildungen das Gibbsche Phänomen deutlich zu sehen.

Abb. 7.7.6: Interpolation der Sprungfunktion (7.7.6) durch ein Polynom zu den 50 auf [0,1] transformierten Tschebyscheff-Abszissen.

Abb. 7.7.7: Interpolation der Sprungfunktion (7.7.6) durch ein Polynom zu den 200 auf [0,1] transformierten Tschebyscheff-Abszissen.

Abb. 7.7.8: Interpolation der Sprungfunktion (7.7.6) durch ein Polynom zu den 4000 auf [0,1] transformierten Tschebyscheff-Abszissen.

Beispiel (Divergenz trotz beliebiger Differenzierbarkeit)
Die Funktion (Runge (345))

$f(x) = \frac{1}{1 + 25x^2} \qquad \mbox{($
ist auf [-1,1] beliebig oft differenzierbar. Die Folge der Interpolationspolynome auf äquidistan- ten Knoten konvergiert jedoch nur für |x| <= 0.726 gegen f und divergiert im übrigen.
Die Werte von P₁₀ liegen ungefähr zwischen -0.30 und 1.95, jene von P₁₆ bereits zwischen -14 und 1.35, obwohl f(x) $\in$ (0.03846,1] gilt. Als Ausdruck der Divergenz tritt mit steigendem Polynomgrad immer stärker werdendes "Überschwingen" in der Nähe der Intervallendpunkte -1 und 1 auf (siehe Abb.7.7.4).
Auch in jenen Teilen des Intervalls [-1,1], wo Konvergenz gewährleistet ist, macht die sehr niedrige Konvergenzgeschwindigkeit den algorithmischen Einsatz äquidistanter Interpolationsknoten äußerst ineffizient.

[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]