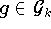 an k Knotenpunkten
an k Knotenpunkten
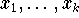 mit k vorgegebenen Werten
mit k vorgegebenen Werten
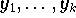 kann man bei allgemeinen
Interpolationsproblemen die Übereinstimmung von
k Funktionalen
kann man bei allgemeinen
Interpolationsproblemen die Übereinstimmung von
k Funktionalen
[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]
Außer der Übereinstimmung der Modellfunktion
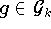 an k Knotenpunkten
an k Knotenpunkten
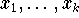 mit k vorgegebenen Werten
mit k vorgegebenen Werten
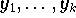 kann man bei allgemeinen
Interpolationsproblemen die Übereinstimmung von
k Funktionalen
kann man bei allgemeinen
Interpolationsproblemen die Übereinstimmung von
k Funktionalen
[ Ein (lineares) Funktional ist eine (lineare) Abbildung eines normierten Raumes in den zugehörigen Grundkörper. So ordnet z.B. ein Funktional, das auf einem Raum der reellen Funktionen definiert ist, jeder Funktion eine reelle Zahl zu. ]
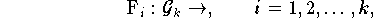
einer Funktion
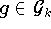 mit vorgegebenen Werten
mit vorgegebenen Werten
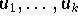 fordern:
fordern:
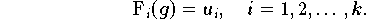
Um die Grundlage für eine effiziente Parameterbestimmung zu schaffen - die
Interpolation wird oft wegen ihres geringeren Rechenaufwandes der
Bestapproximation vorgezogen -, wird im folgenden nur der in der Praxis
besonders wichtige lineare Fall betrachtet: Nur lineare Funktionale
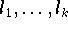 werden der Interpolation zugrunde gelegt, und die Elemente
der k-parametrigen Funktionsklasse
werden der Interpolation zugrunde gelegt, und die Elemente
der k-parametrigen Funktionsklasse
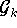 , aus der die Interpolationsfunktion
, aus der die Interpolationsfunktion
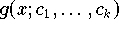 zu bestimmen ist, werden als
linear in ihren Parametern
zu bestimmen ist, werden als
linear in ihren Parametern
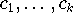 angenommen.
angenommen.