[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]

Das allgemeine Interpolationsprinzip

Alle Interpolationsaufgaben dieses Abschnitts kann man durch das folgende mathematische Problem ausdrücken.

Will man eine gegebene Funktion f durch ein allgemeines Interpolationsproblem mit einer Modellfunktion 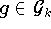approximieren, muß 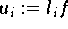gelten. Die linearen Funktionale 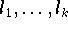müssen in diesem Fall auf einer Funktionenklasse definiert sein, die sowohl 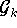, den Raum aller k-parametrigen Approximationsfunktionen, als auch den Funktionenraum 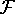, der die möglichen Datenfunktionen f enthält, umfaßt.

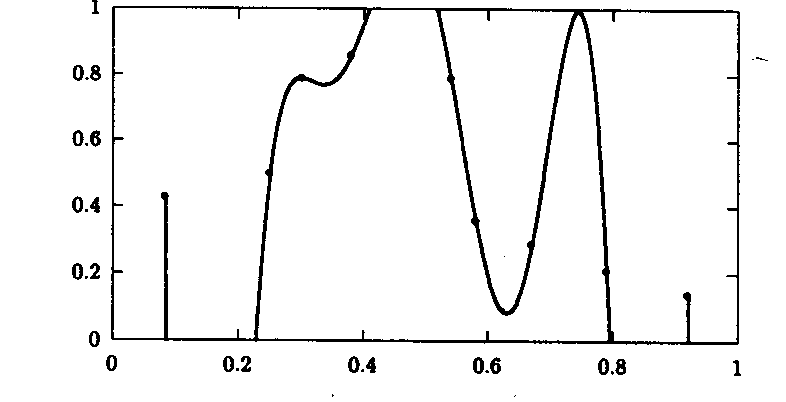
Abbildung: Interpolation von 9 Datenpunkten durch ein Polynom ...

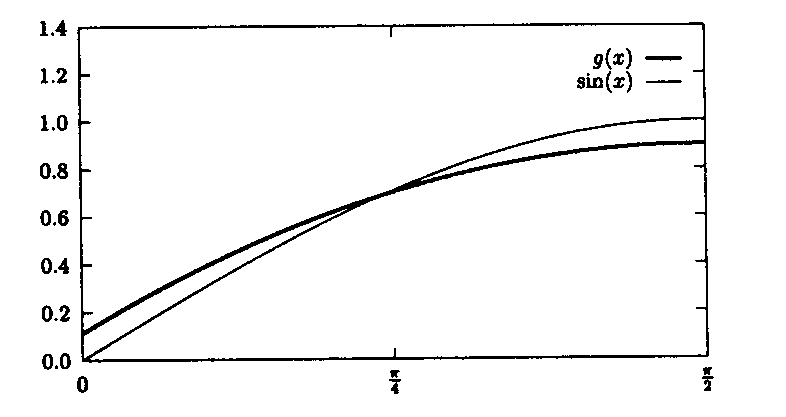
Abbildung: Interpolation bezüglich allgemeiner linearer Funktionale

Dieses Beispiel zeigt, daß es nicht immer Funktionswerte 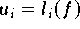sein müssen, die vom Anwender zur Festlegung einer Interpolationsfunktion verwendet werden.

Im Zusammenhang mit dem allgemeinen Interpolationsproblem ergibt sich eine Reihe von Fragen: Unter welchen Voraussetzungen existiert überhaupt eine Lösung des Problems? Falls eine Lösung existiert, ist sie eindeutig oder gibt es mehrere Lösungen? Was kann man über die Approximationsgenauigkeit D(g,f) aussagen, wenn man die Interpolationsfunktion g zur Approximation von f verwendet, wenn man also 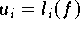annimmt?

Die ersten beiden Fragen kann man für das allgemeine Interpolationsproblem beantworten, für die Beurteilung der Approximationsgenauigkeit muß man zusätzliche Annahmen über 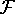, 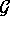und die Funktionale 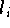treffen, um zu quantitativen Aussagen zu gelangen. Das Thema der Approximationsgenauigkeit wird etwas später (in den Abschnitten Approximations- und Konvergenzeigenschaften und Verfahrensfehler der Polynominterpolation ) genauer diskutiert.

• Eindeutige Lösbarkeit

[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]