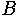 eines Vektorraumes
eines Vektorraumes
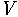 heißt eine Basis von
heißt eine Basis von
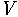 , wenn jeder Vektor
, wenn jeder Vektor
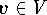 eindeutig in Form einer endlichen
Linearkombination
eindeutig in Form einer endlichen
Linearkombination
[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]
Definition: Basis
Eine Teilmenge
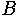 eines Vektorraumes
eines Vektorraumes
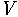 heißt eine Basis von
heißt eine Basis von
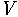 , wenn jeder Vektor
, wenn jeder Vektor
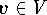 eindeutig in Form einer endlichen
Linearkombination
eindeutig in Form einer endlichen
Linearkombination
von Basiselementen dargestellt werden kann.
Die Skalare
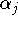 nennt man die Koordinaten des Vektors
nennt man die Koordinaten des Vektors
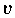 bezüglich der Basis
bezüglich der Basis
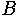 .
.
Läßt sich jeder Vektor
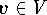 - nicht notwendigerweise
eindeutig - in der
als einem
Erzeugendensystem.
- nicht notwendigerweise
eindeutig - in der
als einem
Erzeugendensystem.
Besitzt ein Vektorraum
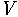 eine endliche Basis, so wird die allen Basen von
eine endliche Basis, so wird die allen Basen von
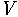 gemeinsamen Anzahl von Basisvektoren
die Dimension von
gemeinsamen Anzahl von Basisvektoren
die Dimension von
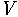 genannt. Besitzt
genannt. Besitzt
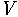 jedoch keine endliche Basis, so heißt
jedoch keine endliche Basis, so heißt
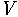 unendlich-dimensional.
unendlich-dimensional.
* * *
Euklidischer Raum
Die Zahlenräume
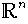 sind endlich-dimensional von der Dimension
n. Sie besitzen z.B. die kanonische Basis
sind endlich-dimensional von der Dimension
n. Sie besitzen z.B. die kanonische Basis
![\[ e_1 = (1,0,\dots,0), \quad e_2 = (0,1,0,\dots,0), \, \dots\,,\,
e_n = (0,\dots,0,1). \]](pic/f04_0124.gif)
* * *
Stetige Funktionen
Der lineare Raum der stetigen Funktionen C[a, b] ist nicht endlich-dimensional, er ist vielmehr ein unendlich-dimensionaler Vektorraum.
* * *
Polynome
Die Menge
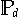 aller Polynome vom Maximalgrad d ist
ein linearer Raum der Dimension d+1;
aller Polynome vom Maximalgrad d ist
ein linearer Raum der Dimension d+1;
hingegen ist die Menge
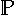 aller Polynome ein unendlich-dimensionaler Vektorraum.
aller Polynome ein unendlich-dimensionaler Vektorraum.
[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]