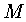 heißt ein linearer Raum oder Vektorraum,
heißt ein linearer Raum oder Vektorraum,
[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]
Definition: Linearer Raum, Vektorraum
Eine Menge
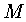 heißt ein linearer Raum oder Vektorraum,
heißt ein linearer Raum oder Vektorraum,
wenn
| 1. | in
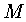 eine Addition definiert ist, für die
eine Addition definiert ist, für die
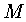 eine abelsche Gruppe bildet,
eine abelsche Gruppe bildet,
|
* * *
Lineare Räume
Die Menge der n-TupeI
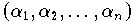 mit reellen
mit reellen
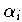 und den Verknüpfungen
und den Verknüpfungen
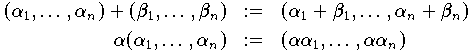
ist ein linearer Raum, der mit
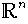 bezeichnet wird. Die übliche Terminologie dieses Raumes, insbesondere die Bezeichnungen
Vektor und Punkt, wird auch bei anderen linearen Räumen
verwendet.
bezeichnet wird. Die übliche Terminologie dieses Raumes, insbesondere die Bezeichnungen
Vektor und Punkt, wird auch bei anderen linearen Räumen
verwendet.
Die Menge aller stetigen Funktionen, die auf einem Intervall [a, b] definiert sind, ist ein linearer Raum, der mit C[a, b] bezeichnet wird.
Die Menge aller auf einem Intervall [a, b] m-mal stetig differenzierbaren Funktionen ist ein linearer Raum, der mit Cm[a,b] bezeichnet wird.
Die Menge aller Funktionen
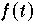 , für die
, für die
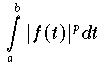 bzw.
bzw.
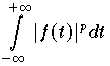 (8.10)
(8.10)
[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]