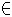[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]

Beispiele zu Optische Form

Sättigungsfunktion

Viele ökonomische und technisch-naturwissenschaftliche Wachstumsphänomene, die mit Funktionen einer Veränderlichen modelliert werden sollen, sind durch Grenzwerte charakerisiert, denen sich beobachtete Werte asymptotisch nähern. Als Modelle eignen sich z.B Sättigungsfunktionen, die ihrem Wesen nach Summen (bzw. Integrale) für gegen Null strebende Zuwachsgrößen sind. In Abb. 6.11 sind Datenpunkte einer symetrischen Sättigungfunktion^* dargestellt. Interpoliert man die 11 Datenpunkte (O) mit einem Polynom vom Grad 10, so erhält man den in Abb 6.12 dargestellten, absolut unbefriedigenden Funktionsverlauf (-). Während für alle Datenpunkte y_i 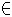[0,1] gilt, nimmt das Polynom Werte

P₁₀(x) 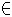[-4700, 4700], x 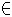[x_min, x_max],

an, die mit dem intuitiv erwarteten Funktionsverlauf (mit Ausnahme einer kleinen Umgebung des Wendepunkts) nichts zu tun haben. Die Akima-Interpolation liefert eine nur einmal stetig differenzierbare Funktion (--), deren Glattheit im mathematischen Sinn deutlich geringer ist als jene des Polynoms, die aber den intuitiven Vorstellungen wesentlich besser entspricht.

* Eine Sättigungsfunktion f ist symetrisch, wenn ihre Zuwachsfunktion f' symetrisch ist.

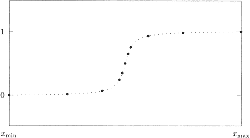
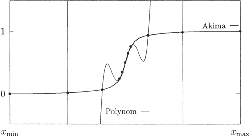
Abb 611 und Abb 6.12

[<< Zurück zum Text]

[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]