[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]

[Thomas Stockinger]

6.1 Analytische Modelle

6.1 Analytische Modelle

Ziel der analytischen Modellbildung ist die Gewinnung von Funktionen

$f:B\subset \Re ^n\rightarrow \Re $,

deren Definitionsbereich B eine zusammenhängende Teilmenge des 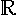$\R $n , also z.B. ein endliches oder auch unendliches Intervall, ist. Abhängig von der Dimension n des Definitionsbereichs B unterscheidet man

univariate Modelle mit einer unabhängigen Variable (n=1) und

multivariate Modelle mit mehreren unabhängigen Variablen (n>1).

Es wird jedoch bei der Modellbildung keine strukturelle Analogie zwischen Objekt und Modell gefordert, d.h. es werden nur Funktionsmodelle betrachtet, die

  1. das gegebene Objekt oder Phänomen bzw. die Information darüber in einem noch zu präzisierenden Sinn (siehe Wahl der Distanzfunktion) quantitativ adäquat beschreiben und die
  2. als analytische Daten darstellbar und verarbeitbar sind, d.h. die gesuchten Funktionen müssen auf einem Computer numerisch gespeichert und algorithmisch verarbeitet werden können. Das sind z.B. Polynome, lineare Gleichungen usw. (siehe elementare Funktionen)

Wie in der obigen Formel zur Modellbildung ersichtlich, handelt es sich um Funktionen, die jedem Element x ihres Definitionsbereichs B genau ein Element ihres Wertebereichs zuordnen. Falls als Modell Kurven und Flächen im Raum in Betracht gezogen werden, können auch diese durch Modellfunktionen dargestellt werden.

Beispiel (Raumkurve) Eine Kurve im 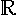$\R $3, die durch die Punkte

Pi=(ui , vi , wi ) 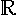$\in $ $\R $3,      i=1,2,3,...,k

verläuft, kann durch drei interpolierende Funktionen f u(s), f v(s) und f w(s) modelliert werden, wobei folgende Bedingung erfüllt sein muß:

$f(s_i)=\left( \matrix f_u(s_i) \\ f_v(s_i) \\ f_w(s_i)\endmatrix \right)=\left( \matrix u_i \\ v_i \\ w_i\endmatrix \right)=P_i\,i=1,2,...,k$

6.1.1 Elementare Funktionen als Modelle

Wie bereits angesprochen, wird durch die Forderung nach der Verarbeitbarkeit der Modelle auf einem Computer das Ergebnis eines kontinuierlich-funktionalen Modellierungs- bzw. Approximationsprozesses auf elementare Funktionen eingeschänkt.

Definition: Elementare Funktionen lassen sich durch eine endliche Anzahl von Parametern charakterisieren. Sie sind durch Formeln definierbar, in denen nur endlich viele Auswertungen der auf einem Computer verfügbaren Standardfunktionen (algebraisch, trigonometrisch oder logarithmisch) und allenfalls Fallunterscheidungen durch bedingte Anweisungen (z.B. bei stückweise definierten Funktionen) auftreten.

Als Modell- bzw. Approximationsfunktionen kommen zum Beispiel in Frage:

Funktionen, die diese Forderung nicht erfüllen, weil sie z.B. unendlich viele Koeffizienten einer Taylor-Reihe zu ihrer Charakterisierung benötigen, müssen durch elementare Funktionen approximiert (modelliert) werden.

Elementare Funktionen für analytische Operationen

Die Klasse der elementaren Funktionen kann für verschiedene Aufgabenstellungen noch immer zu umfassend sein. Eine besonders wichtige Modellbildungssituation, wo oft weitere Einschränkungen erforderlich sind, bilden numerische Verfahren zur Lösung mathematischer Probleme wie z.B. Integration, Differentiation etc. Diese Probleme nönne im allgemeinen nicht direkt gelöst werden. Konstruktive Lösungsmethoden erfordern daher (oft automatisch-algorithmitsch ablaufende) Modellbildungs- bzw. Approximationsvorgänge:

  1. Das ursprüngliche Problem wird durch ein Modellproblem esetzt.
  2. Berechnung einer numerischen Lösung des Ersatz- bzw. Modellproblems.
  3. Die Lösung des Modellproblems wird als Näherung (Schätzung) für die Lösung des Originalproblems verwendet.

Dabei ist die Wahl einer geeigneten Klasse von Ersatzfunktionen stark von den Besonderheiten der jeweiligen Problemstellung abhängig. Eine universelle Regel ist:

Bei numerischen Verfahren am häufigsten verwendete Klasse elementarer Funktionen ist die der Polynome, da diese bei den meisten Aufgabenstellungen eine exakte und mit geringem Rechenaufwand verbundene Lösung erlauben.

Beispiel: Die Ermittlung von Extremwerten (Maxima, Minima, Nullstellen) analytischer Daten eines mathematischen Problems am Computer ist auf der Basis einer Nullstellenbestimmung der ersten Ableitung meist nicht direkt möglich. Die Funktion, deren Extrema gesucht sind, muß durch geeignete Modellfunktionen ersetzt werden, die eine einfache und exakte Extremwertbestimmung erlauben. Im univariaten Fall sind dies vorzugsweise quadratische Polynome:

Beschreibung: Eine gegebenen Funktion wird diskretisiert und anhand der Diskretisierungspunkte ein quadratisches Polynom interpoliert. Der Extremwert des Interpolationspolynoms wird bestimmt und als Näherung für das gesuchte Minimum verwendet.

In den folgenden Kapiteln wird auf diese Vorgänge (Diskretisierung, Homogenisierung) weiter eingegangen.

6.1.2 Algorithmen als Modelle

Im Unterschied zu den elementaren Funktionen geschieht bei der Darstellung und Implementierung von Modellen mit Hilfe von Operatorgleichungen die Auswertung konkreter Werte nicht formelartig, sondern iterativ/prozeßartig. Die numerischen Werte hängen daher unter anderem von der Konvergenzgeschwindigkeit des Iterationsverfahren an der Stelle der Auswertung, vom Abbruchkriterium (der geforderten Approximationsgenauigkeit) oder der aktuellen Maschinenarithmetik ab.

Beispiel: Quadratwurzelfunktion
Die Standardfunktion $f(x)=\sqrt{x}$ wird nicht mit Hilfe einer Approximationsfunktion implementiert, sondern durch einen Algorithmus, der die iterative Lösung der Gleichung (bzw. des Nullstellenproblems) $g^2-x=0$ beschreibt.

Bei diesem Algorithmus wird zunächst der Exponent e(x) halbiert und anschließend das Newton-Verfahren zur Bestimmung der Quadratwurzel der Mantisse mx := M(x) der Gleitpunktzahl x angewendet, d.h. $g^2-m_x=0$ wird iterativ gelöst:

$g_i:=\frac{g_{i-1}+\frac{m_x}{g_{i-1}}}2\quad \quad i=1,2,3,...,i_{\max }$

Dies wird solange fortgesetzt, bis ein gefordertes Abbruchkriterium, also z.B. $\left| g_j-g_{j-1}\right| <\delta $,eintritt, bzw. bis imax erreicht wird, das genauso wie die Startnäherung g0 abhängig von der Maschinenarithmetik gewählt wird.

[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]