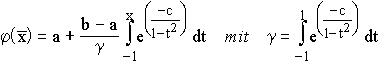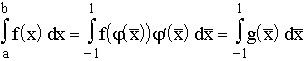[ < ]
[ globale Übersicht ]
[ Kapitelübersicht ]
[ Stichwortsuche ]
[ > ]
Inhaltsverzeichnis Kapitel 7.4.4 Interpolatorische Quadraturformeln
7.4.4.3 Zusammengesetzte Qaudraturformeln
7.4.4.3.1 Allgemeines
7.4.4.3.2 Konvergenz
7.4.4.3.3 Zusammengesetzte Trapezregel
Beispiel für die zusammengesetzte Trapezregel
7.4.4.3.4 IMT-Formeln
7.4.4 Interpolatorische Quadraturformeln
In den vorigen Kapiteln wurden verschiedene einfache interpolatorische
Quadraturformeln besprochen, also solche, die durch Integration eines Interpolationspolynoms
auf dem Integrationsintervall zustande kamen. In diesem Abschnitt sollen
nun Formeln diskutiert werden, die man durch Integration eines stückweisen
Polynoms erhält. Äquivalent zu diesem Zugang ist die Unterteilung
des Intervalls [a,b] in Teilintervalle, auf die dann jeweils eine einfache
interpolatorische Formel angewandt wird. Von zentraler Bedeutung für
die numerische Integration ist der Umstand, daß ein bestimmtes Integral
über einem Intervall [a,b] als Integralen über disjunkte Teilintervalle
additiv zusammengesetzt werden kann.
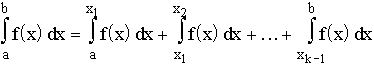
In diesem Abschnitt wird angenommen, daß [a,b] durch die Teilungspunkte
a = x0 < x1
< ... < xk
= b in k äquidistante Teilintervalle zerlegt wird (Nichtäquidistante
Unterteilungen von [a,b] werden im Zusammenhang mit Integrationsalgorithmen
behandelt). In jedem dieser k Teilintervalle wird die gleiche einfache
N-Punkt-Quadraturformel QN angewendet.
Die sich damit ergebende zusammengesetzte Quadraturformel wird mit k
x QN bezeichnet.
In jenen Fällen, wo QN eine abgeschlossene
Formel ist - bei der also beide Intervallendpunkte Quadraturabszissen sind
- ist die Anzahl k(N - 1) + 1 der Abszissen der zusammengesetzten
Formel k x QN niedriger als k . N, da
die Abszissen an den Intervallgrenzen x1,
x2, ...
, xk - 1 nur einmal zu zählen
sind, weil dort nur ein f-Wert benötigt wird.
Im Gegensatz zu den einfachen Quadraturformeln konvergieren zusammengesetzte
Quadraturformeln für alle Riemann-integrierbaren Funktionen.
Satz: Sei QN eine N-Punkt-Quadraturformel
mit einem Genauigkeitsgrad D >= 0, d. h. f = 1 wird von QN
exakt integriert. Dann gilt für jede auf [a,b] beschränkte, Riemann-integrierbare
Funktion (k x QN) f --> If für k --> unendlich.
Dieser Satz liefert ein starkes Argument für die Verwendung zusammengesetzter
Formeln. Ein weiterer Vorteil des Formelzusammensetzens ist die Möglichkeit
der ungleichmäßigen adaptiven Gitterverfeinerung (Diskretisierungs-Strategie).
Fast alle Computerprogramme zur numerischen Quadratur beruhen in irgendeiner
Form auf zusammengesetzte Formeln.
Eine wichtige Integrationsformel ist die zusammengesetzte Trapezregel
Tl = l x T,
![$T_lf=h\left[ \frac 12f(a)+f(a+h)+...+f(a+(l-1)h)+\frac 12f(b)\right] $](pic/g04_0431.gif)
Den Fehler der (l + 1)-Punkt-Formel Tl
kann man - bei ausreichender Differenzierbarkeit der Integrandenfunktion
f - sehr genau charakterisieren.
Satz: (Euler-Maclaurinsche Summenformel): Es gilt die Fehlerformel
![$\matrix T_lf-If= & \frac{B_2}{2!}h^2\left[ f^{(1)}(b)-f^{(1)}(a)\right] + \\ & +\frac{B_4}{4!}h^4\left[ f^{(3)}(b)-f^{(3)}(a)\right] +...+ \\ &+\frac{B_{2k}}{\left( 2k\right) !}h^{2k}\left[f^{(2k-1)}(b)-f^{(2k-1)}(a)\right] + \\ & +h^{2k+1}\int\limits_a^b\barP_{2k+1}\left( l\frac{x-a}{b-a}\right) f^{(2k+1)}dx, \\ \text{f\](pic/g04_0432.gif)
wobei die Konstanten die Bernoulli-Zahlen B2 = 1/6,
B4 = -1/30, B6 = 1/42, B8
= -1/30, B10 = 5/66, ... sind. Die Funktion P2k
+ 1 ist durch folgende Reihe definiert:
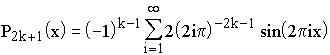
Der Fehlerformel kann man insbesondere entnehmen, daß für
Integranden, deren ungerade Ableitungen an den beiden Endpunkten des Integrationsintervalls
übereinstimmen, z. B. bei allen (b - a)-periodischen Integranden,
die zusammengesetzte Trapezregel Tl besonders
genaue Resultate liefert.
Wendet man Tl auf Integranden
![$\matrix f\in C^{2k+1}\left[ a,b\right] & \text{mit} \\f^{(1)}(a)=f^{(1)}(b),...,f^{(2k-1)}(a)=f^{(2k-1)}(b) & \text{und} \\ \left|f^{(2k+1)}(x)\right| \leq M_{2k+1},\forall x\in \left[ a,b\right] & \text{an,dann gibt} \\ \left| T_if-If\right| \leq Ch^{2k+1},\quad h=\frac{b-a}l &\endmatrix $](pic/g04_0434.gif)
die Konvergenzordnung von Tlf --> If an.
Beispiel (zusammengesetzte Trapezregel)
Dieses Verfahren soll in Form eines interaktiven Beispiels gezeigt werden.
Die rasche Konvergenz der zusammengesetzten Trapezregel kann man auch
für nichtperiodische Integrandenfunktionen erreichen, wenn man eine
geeignete periodisierende Variablentransformation durchführt (Transformation
von Integralen).
Eine Subsitution, die der transformierten Funktion g die Eigenschaft
g(i) (-1) = g(i) (1) = 0, j = 1, 2, ... ,
gibt, ist die - geeignet skalierte - IMT-Transformation
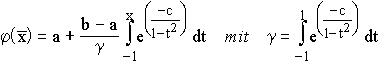
Die Parameter c kann aus R+ gewählt
werden, wobei sich der Wert c = 4 praktisch bewährt hat.
Mit der Transformation erhält man
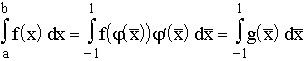
Drückt man Tlg in f aus, so erhält
man Quadraturformeln QN mit N = l +1
Abszissen, die trotz ihrer Herkunft von der l-fach zusammengesetzten
Trapezregel Tl einfach
und nicht zusammengesetzt sind. Sie werden wegen Verwendung der IMT-Transformation
als IMT-Formeln bezeichnet und haben folgende Vorteile:
- Auf Grund der speziellen Transformation g und des Nichtauftretens
der Randabszissen in QN sind sie für Integranden
mit (integrierbaren) Singularitäten and den Intervallgrenzen a
und b gut geeignet. Dies gilt insbesondere auch für Integrale
auf unendlichen Bereichen (a = - unendlich und/oder b = unendlich),
die auf einen endlichen Bereich transformiert wurden, wodurch sich im allgemeinen
Endpunktsingularitäten einstellen (Transformation von Integralen).
- Für eine Folge {QN} von Formeln mit
N = 1, 2, 3, ... können bei der Auswertung von QN
alle Funktionswerte der vorangegangenen Formeln der Folge wiederverwendet
werden, was sich günstig auf die Effizienz auswirkt.
[ < ]
[ globale Übersicht ]
[ Kapitelübersicht ]
[ Stichwortsuche ]
[ > ]
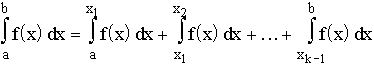
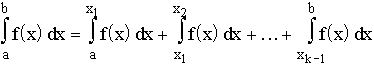
![$T_lf=h\left[ \frac 12f(a)+f(a+h)+...+f(a+(l-1)h)+\frac 12f(b)\right] $](pic/g04_0431.gif)
![$\matrix T_lf-If= & \frac{B_2}{2!}h^2\left[ f^{(1)}(b)-f^{(1)}(a)\right] + \\ & +\frac{B_4}{4!}h^4\left[ f^{(3)}(b)-f^{(3)}(a)\right] +...+ \\ &+\frac{B_{2k}}{\left( 2k\right) !}h^{2k}\left[f^{(2k-1)}(b)-f^{(2k-1)}(a)\right] + \\ & +h^{2k+1}\int\limits_a^b\barP_{2k+1}\left( l\frac{x-a}{b-a}\right) f^{(2k+1)}dx, \\ \text{f\](pic/g04_0432.gif)
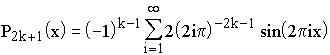
![$\matrix f\in C^{2k+1}\left[ a,b\right] & \text{mit} \\f^{(1)}(a)=f^{(1)}(b),...,f^{(2k-1)}(a)=f^{(2k-1)}(b) & \text{und} \\ \left|f^{(2k+1)}(x)\right| \leq M_{2k+1},\forall x\in \left[ a,b\right] & \text{an,dann gibt} \\ \left| T_if-If\right| \leq Ch^{2k+1},\quad h=\frac{b-a}l &\endmatrix $](pic/g04_0434.gif)