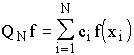[ < ]
[ globale Übersicht ]
[ Kapitelübersicht ]
[ Stichwortsuche ]
[ > ]
Inhaltsverzeichnis Kapitel 7.4.4 Interpolatorische Quadraturformeln
7.4.4.2 Einfache interpolatorische Quadraturformeln
7.4.4.2.1 Allgemeines
7.4.4.2.2 Newton-Cotes-Formeln
7.4.4.2.3 Clenshaw-Curtis-Formeln
7.4.4.2.4 Gauß-Formeln
7.4.4.2.5 Radau- und Lobatto-Formeln
7.4.4.2.6 Gauß-Konrod-Formeln
7.4.4.2.7 Patterson-Formeln
7.4.4 Interpolatorische Quadraturformeln
Durch die Wahl der Abszissen (Stützstellen) x1,x2,...,xN sind die Quadraturformeln QN nicht
nur eindeutig festgelegt, sondern lassen sich dadurch auch in verschiedene Formel-Familien einteilen.
Um nun die einzelnen Vor- und Nachteile dieser Familien genauer zu erläutern, werden gewisse
Einteilungskriterien benötigt. Das erste Kriterium ist der
Genauigkeitsgrad
Definition (Genauigkeitsgrad):
Eine Quadraturformel QN hat den Genauigkeitsgrad D, wenn

und

gilt, d.h., falls QN alle Polynome bis zum Maximalwert D exakt integriert und es ein Polynom vom
Grad D+1 gibt, das von QN nicht mehr exakt integriert wird.
Satz:
Jede N-punktige Quadraturformel QN mit einem Genauigkeitsgrad D>=N-1 (aufgrund ihrer Konstruktion) ist
eine interpolatorische Formel.
Es sei PD die Menge aller approximierenden Polynome
Satz:
Für eine interpolatorische Quadraturformel QN mit dem Genauigkeitsgrad D gilt die Fehlerabschätzung

mit

Falls QN nur positive Quadraturgewichte besitzt, gilt
 .
.
Ein weiteres wichtiges Einteilungskriterium ist die
Besitzt eine Folge von Quadraturformeln {QN} nur positive Gewichte für alle N,
dann ist die Konvergenz für alle f Element aus C[a,b] gültig aufgrund der
vorherigen Fehlerabschätzung. Weiters läßt sich daraus schließen, daß
(bei gleicher Stützstellenzahl) Formeln mit einem höheren Genauigkeitsgrad eine kleinere
Fehlerschranke besitzen.
Ohne weitere Informationen lassen sich aber keine Aussagen über die Konvergenzgeschwindigkeit
(wie rasch eine Folge gegen einen gewissen Endwert konvergiert) der Folge {QNf} machen.
Vorstellung der wichtigsten einfachen Quadraturformeln
Allen Newton-Cotes-Formeln, egal ob abgeschlossen oder offen, besitzen eine äquidistante
Unterteilung des Intervalls [a,b] in n Teilintervalle mit N Abszissen (Stützstellen).
Je nachdem, ob nun die Endpunkte a und b ihrerseits selbst die äußersten Abszissen
sind unterscheidet man in die abgeschlossenen und die offenen Newton-Cotes-Formeln.
Wichtig anzumerken ist, daß bei den abgeschlosenen Newton-Cotes-Formeln bei einem Genauigkeitsgrad D=8 und bei allen Formeln
(abgeschlossene und offene Newton-Cotes-Formeln) mit D größer gleich 10 negative Koeffizienten auftreten. Während
bei interpolatorischen Quadraturformeln mit positiven Koeffizienten die Beziehung

gilt (da f=1 exakt integriert wird) ist dies bei den höheren Newton-Cotes-Formeln nicht der Fall.
Es gilt sogar folgender Satz:
Satz (Kusmin): Ist I:=[a,b] ein abgeschlossenes Intervall der reellen Zahlen und ist

für jedes N eine Interpolationsquadratur für äquidistante Punkte, so strebt die Summe
 für
für 
gegen Unendlich.
Das Anwachsen der Summe der Beträge derKoeffizienten für steigendes N führt unter anderem dazu,
daß Fehler (Störungen) des Funktionswertes f(xi) um den Faktor ciN
verstärkt in das Resultat QNf Eingang finden. Somit sind die Newton-Cotes-Formeln für große Werte von
N nicht stabil.
Um nun den Verfahrensfehler unter jede vorgebbare Toleranz zu bringen, muß die Konvergenz
 , für
, für  gewährleistet sein.
gewährleistet sein.
Bei den abgeschlossenen Newton-Cotes-Formeln sind die Intervallendpunkte a, b selbst Quadraturabszissen
(Stützwerte).
Die einzelnen Abszissen
 haben dabei die Abstände
haben dabei die Abstände
 .
Die Gewichte ci ergeben sich dabei durch die Integration der Langrangeschen Elementarpolynome
.
Die Gewichte ci ergeben sich dabei durch die Integration der Langrangeschen Elementarpolynome
 .
Mit der Ersetzung von
.
Mit der Ersetzung von
![$Q_nf=\sum\limits_{i=1}^N\left[ \left( h\cdot\int\limits_0^{N-1}\prod\limits\Sb j=1 \\ j\neq i\endSb^N\frac{t-j+1}{i-j}dt\right) \cdot f_i\right] $$x=a+th\quad \Rightarrow \quad t=\frac{x-a}{b-a}(N-1)$](pic/g04_0421.gif) und den eingesetzten Abszissenwerten xi ergeben sich folgende Gewichte
und den eingesetzten Abszissenwerten xi ergeben sich folgende Gewichte
 .
Die daraus resultierende allgemeine Form der Abgeschlossenen Newton-Cotes-Formel mit
fi=f(xi) lautet somit
.
Die daraus resultierende allgemeine Form der Abgeschlossenen Newton-Cotes-Formel mit
fi=f(xi) lautet somit
![$Q_nf=\sum\limits_{i=1}^N\left[ \left( h\cdot\int\limits_0^{N-1}\prod\limits\Sb j=1 \\ j\neq i\endSb^N\frac{t-j+1}{i-j}dt\right) \cdot f_i\right] $](pic/g04_0423.gif) .
Berechnet man nun die abgeschlossenen Newton-Cotes-Formeln für die ersten drei Werte von N (2,3,4), so erhält man folgende Formeln:
.
Berechnet man nun die abgeschlossenen Newton-Cotes-Formeln für die ersten drei Werte von N (2,3,4), so erhält man folgende Formeln:

Hierbei sei noch angemerkt, daß im Falle der Trapezregel durch die Interpolation mit einem Polynom ein Trapez entsteht,
welches von den Geraden x1=a, x2=b, der Strecke auf der x-Achse zwischen x1 und x2
sowie der Sehne zwischen (a,f(a)) und (b,f(b)) begrenzt wird. Die Fläche dieses Trapezes wird als Näherung für den
gesuchten Integralwert verwendet.
Ebenfalls sei erwähnt,daß sich die Simpsonregel aufgrund der auf Kepler zurückgehende Näherungsformel
 ,
,
welche auch als Keplersche Faßregel bekannt ist, entwickelt hat. Man erhält sie, wenn man durch die Punkte
(a, f(a)), ([a+b]/2, f([a+b]/2)) und (b, f(b)) eine quadratische Parabel legt und diese als
Näherung für f im Intervall [a, b] verwendet. Wird nun das Intervall [a, b] in eine gerade Anzahl von Teilintervallen
zerlegt und in je zwei aufeinanderfolgenden Intervallen die Funktion f durch eine quadratische Interpolationsparabel angenähert,
so kommt man am Ende auf die Simpsonregel.
Beispiel (Trapezregel und Keplersche Faßregel)
Diese beiden Verfahren sollen in Form eines interaktiven Beispiels gezeigt werden.
Offene Newton-Cotes Formeln:
Den offenen Newton-Cotes-Formeln liegen die Quadraturabszissen

zugrunde.
Die Bezeichnung "offen" weist darauf hin, daß die
Endpunkte a und b des Integrationsintervalles in diesem Fall keine Quadraturabszissen
sind. Die ersten drei offenen Newton-Cotes-Formeln lauten:
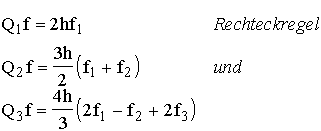
7.4.4.2.3 Clenshaw-Curtis-Formeln:
Bei der Approximation durch Interpolationspolynome ist die Wahl der
Tschebyscheff-Abszissen den äquidistanten Abszissen deutlich überlegen.
Es ist daher zu erwarten, daß sich die Tschebyscheff-Nullstellen
und Extrema auch als Quadraturabszissen gut bewähren. Dies ist tatsächlich
der Fall; sowohl die Tschebyscheff-Nullstellen (klassische Clenshaw-Curtis-Formeln)
 ,
als auch die Tschebyscheff-Extrema (praktische Clenshaw-Curtis-Formeln)
,
als auch die Tschebyscheff-Extrema (praktische Clenshaw-Curtis-Formeln)
 des Tschebyscheffpolynoms
des Tschebyscheffpolynoms
 mit i = 1, 2, 3, ... , N, führen auf interpolatorische Quadraturformeln
mit positiven Gewichten. In beiden Fällen ist somit die Konvergenz
QNf --> If, mit N --> unendlich
gesichert.
mit i = 1, 2, 3, ... , N, führen auf interpolatorische Quadraturformeln
mit positiven Gewichten. In beiden Fällen ist somit die Konvergenz
QNf --> If, mit N --> unendlich
gesichert.
Der Genauigkeitsgrad ist allerdings nur D = N -1. Die Tschebyscheff-Extrema
sind den Tschebyscheff-Nullstellen praktisch überlegen, da sie beim
Übergang von QN auf Q2N - 1 nur
die Ermittlung von N - 1 zusätzlichen Werten von f erfordern;
bei Verwendung der Tschebyscheff-Nullstellen müßte man hingegen
beim Übergang von QN auf Q2N alle
2N f-Werte neu berechnen. Man bezeichnet daher die Tschebyscheff-Extrema
als die "praktischen" Clenshaw-Curtis-Abszissen.
7.4.4.2.4 Gauß-Formeln:
Zu beliebig vorgegebenen N Abszissen hat die zugehörige interpolatorische
Quadradurformel QN einen Genauigkeitsgrad D >=
N - 1. Sie wird aber im allgemeinen keinen höheren Genauigkeitsgrad
als N - 1 besitzen, da man bei vorgegebenen Abszissen lediglich
die verbleibenden N Parameter (die Integrationskoeffizienten) so wählen
kann, daß Polynome mit maximal N Parametern (den Polynomkoeffizienten),
d.h. Polynome vom Maximalgrad N - 1, exakt integriert werden.
Den größtmöglichen Genauigkeitsgrad einer N-punktigen Formel
kann man erreichen, wenn alle 2N Parameter - N Koeffizienten und N Abszissen
- geeignet gewählt werden. Auf diese Weise kann man Polynome mit maximal
2N Parametern (d.h. Polynome vom Maximalgrad 2N - 1) exakt integrieren.
Satz: Eine N-punktige Quadraturformel
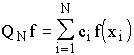
kann höchstens den Genauigkeitsgrad D = 2N - 1 haben. Diesen Genauigkeitsgrad
erreicht man, wenn man als Abszissen x1,
x2, ... , xN
die Nullstellen des N-ten orthogonalen Polynoms (vom Grad d = N)
bezüglich der Gewichtsfunktion w in [a,b] wählt und die Formel
interpolatorisch ist.
Für [a,b] = [-1,1] und w(x) = 1 sind die "optimalen"
Abszissen x1,
x2, ... , xN
die Nullstellen des Legendre-Polynoms vom Grad d = N. Für
ein beliebiges Intervall [a,b] müssen die Abszissen und Gewichte transformiert werden. Die so erhaltenen Quadraturformeln
GN nennt man Gauß-Formeln oder Gauß-Legendre-Formeln.
Die Bezeichnung Gauß-Legendre-Formeln dient dazu,Verwechslungen
mit den Gauß-Laguerre-, Gauß-Hermite- und Gauß-Jacobi-Formeln
zu vermeiden, die man mit den Laguerre-, Hermite- bzw. Jacobi-Gewichtsfunktionen
erhält.
Satz: Die Koeffizienten c1,
c2, ... , cN
der Gauß-Formeln GN sind alle positiv:
ci >
0; i = 1, 2, ... , N; N = 1, 2, 3, ... .
Auf Grund der positiven Gewichte der Gauß-Formeln läßt
sich sofort mit Hilfe des Satzes für die Fehlerschätzung auf die Konvergenz GNf
--> If, N --> unendlich, für alle f
aus C[a,b] schließen. Die Konvergenz der Gauß-Formeln ist sogar
für alle auf [a,b] Riemann-integrierbaren Funktionen f gewährleistet:
Satz: Alle Gauß-Formeln GN,
N = 1, 2, 3, ... , sind Riemann-Summen.
7.4.4.2.5 Radau- und Lobatto-Formeln:
Während bei den Gauß-Formeln alle 2N
zur Verfügung stehenden Parameter (N Gewichte und N
Abszissen) einer N-Punkt Quadraturformel genutzt wurden, um den
maximalen Genauigkeitsgrad D = 2N - 1 zu erreichen, werden bei den
Radau- und Lobatto-Formeln einzelene Abszissen a priori vorgeschrieben.
Die verbleibenden Abszissen und sämtliche Gewichte werden so bestimmt,
daß die entstehenden Formeln größtmöglichen Genauigkeitsgrad
D erhalten.
Bei den Radau-Formeln wird eine Abszisse vorgeschrieben,
und zwar entweder der linke Randpunkt x1
= a oder der rechte Randpunkt xN
= b. Mit den verbleibenden 2N - 1 Parametern werden Formeln vom
Genauigkeitsgrad D = 2N - 2 konsturiert. Bei den Lobatto-Formeln
werden zwei Abszissen vorgeschrieben: die beiden Randpunkte x1
= a und xN = b. Man
erhält auf diese Weise Formeln vom Genauigkeitsgrad D = 2N - 3.
Da sowohl Radau- als auch Lobatto-Formeln wegen ihres hohen Genauigkeitsgrades
interpolatorisch sein müssen, sind diese Formeln durch die Angabe
ihrer Abszissen eindeutig charakterisiert. Die Bedeutung der Radau- und
der Lobatto-Formeln liegt nicht so sehr im Bereich der Quadratur, sondern
eher bei der Integration von Differentialgleichungen und bei der Lösung
von Integralgleichungen, wo sie die Grundlage wichtiger Verfahren mit hoher
Konvergenzordnung bilden.
7.4.4.2.6 Gauß-Kronrod-Formeln:
Bei der praktischen Lösung von Integrationsproblemen haben Gauß-Formeln
einen gravierenden Nachteil: Zwei beliebige Gauß-Formeln
GN und GK mit N
> K haben keine Abszissen gemeinsam (außer eventuell den Intervallmittelpunkt).
Es gibt daher keine effiziente Methode, um zu einer praktisch berechenbaren
Fehlerabschätzung zu gelangen. Die übliche Vorgangsweise, Formeln
mit verschiedener Punktezahl auszuwerten und die Differenz als Fehlerabschätzung
zu verwenden, würde zu viele Werte des Integranden benötigen und
damit einen zu hohen Aufwand verursachen.
Dieser Nachteil der Gauß-Formeln konnte durch eine naheliegende (aber
erst 1965 durch A.S.Kronrod publizierte) Vorgehensweise überwunden
werden. Man gibt (ähnlich wie bei der Konstruktion der Radau-
und Lobatto-Formeln die N Abszissen von GN
fest vor und konstruiert eine (2N + 1)-Punktformel, die den größtmöglichen
Genauigkeitsgrad D = 3N + 1 (N gerade) bzw. D = 3N + 2
(N ungerade) besitzt. Die neuen Abszissen liegen in den Intervallen
(a,x1), (x1,x2),
(x2,x3),
... , (xN,b), wobei die
x1, x2,
... , xN Abszissen von GN
sind.
7.4.4.2.7 Patterson-Formeln:
Die von Kronrod stammende Idee der Erweiterung
von Gauß-Formeln wurde von Patterson aufgegriffen,
der auf die erste Erweiterung von GN auf K2N
+1 noch eine Erweiterung um 2N + 2 zusätzlichen
Abszissen folgen ließ, um so eine Formel vom Genauigkeitsgrad 6N
+ 4 zu erhalten. Auf diese Weise wurde z. B. eine Folge von 3-, 7-,
15-, 31-, 63-, 127-, und 255-Punkt-Formeln konstruiert.
[ < ]
[ globale Übersicht ]
[ Kapitelübersicht ]
[ Stichwortsuche ]
[ > ]





 .
.

 für
für 
 , für
, für 

 .
. .
.![$Q_nf=\sum\limits_{i=1}^N\left[ \left( h\cdot\int\limits_0^{N-1}\prod\limits\Sb j=1 \\ j\neq i\endSb^N\frac{t-j+1}{i-j}dt\right) \cdot f_i\right] $$x=a+th\quad \Rightarrow \quad t=\frac{x-a}{b-a}(N-1)$](pic/g04_0421.gif)
 .
.![$Q_nf=\sum\limits_{i=1}^N\left[ \left( h\cdot\int\limits_0^{N-1}\prod\limits\Sb j=1 \\ j\neq i\endSb^N\frac{t-j+1}{i-j}dt\right) \cdot f_i\right] $](pic/g04_0423.gif) .
.


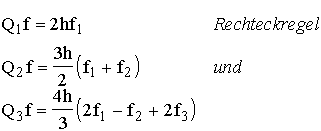
 ,
,