[ < ]
[ globale Übersicht ]
[ Kapitelübersicht ]
[ Stichwortsuche ]
[ > ]
7.2.4 Kondition
Die absolute Konditionsabschätzung des Integralwerts If
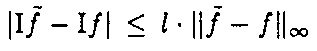
zeigt, daß das mathematische Problem bezüglich der Änderung der Integrandenfunktion eine sehr gute absolute Kondition aufweist. Diese Tatsache rechtfertigt die Ersetzung der zu integrierenden Funktion durch eine vereinfachte Funktion (z.B.: Polygonzug).
Bei der relativen Kondition
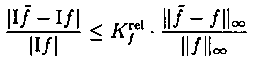
kommt es genau dann zu einer hohen, also sehr schlechten Konditionzahl, wenn die Integrandenfunktionen f sehr groß ist und der Integralwert If einen sehr kleinen Betrag hat.
Ist f sehr groß, so wird der Wert des rechten Bruches sehr klein. Ist If sehr klein, so wird der linke Teil des Bruches groß, da If im Nenner steht. Damit benötigt man ein großes K um die Ungleichung zu erfüllen, d.h. die Konditionzahl ist schlecht.
Im folgenden Beispiel betrachten wir ein Integral, das für m = 2, 4, 6, ... exakt den Wert 0 annimmt.
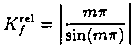
Betrachtet man nun die relative Kondition des Integralwerts bezüglich einer additiven Störung f:=f+d, so ergibt sich für m ungefähr 2k folgendende asymtotische Näherung.
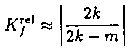
Wenn m ungefähr den Wert 20 annimmt, ergeben sich folgende Werte.

Die Kondition bezüglich der Änderung des Integrationsbereiches ist im Vergleich zur Änderung der Integrandenfunktion unter Umständen bedeutend ungünstiger.
So ist, zum Beispiel bei einer Sigularität (d.h. bei univariaten Funktionen ändert sich die 1.-te Ableitung auf einen kurzen Intervall sehr stark, z.B. 1/n, Polstellen) des Integrationsbereiches nahe dem Rand, die Konditionszahl sehr groß.
In diesem Beispiel betrachten wir das Integral
![\mbox{I}(f;[0,b]) := \int \limits_{0}^{b} (1-x)^{-0.9} \,dx =
-10 (1-b)^{0.1} + 10](pic/g02_0406.gif)
Es reagiert empfindlich auf die Änderung der oberen Grenze b, wenn sie nahe bei 1 liegt.
![\begin{tabular}{|l|llll|}
\hline
\strutHline
$ b $ & $1-10^{-5}$ & $1-10^{-10}$ & $1-10^{-15}$ & $1-10^{-20}$ \\
\hline
\strutNachHline
I$(f;[0,b])$ & 6.8377 & 9.0000 & 9.6838 & 9.9000 \\
\strutVorHline
$K_{0,b} = f(b)$ & $ 3.16 \cdot 10^{4} $ & $ 1.00 \cdot 10^{9} $ &
$ 3.16 \cdot 10^{13} $ & $ 1.00 \cdot 10^{18} $ \\
\hline
\end{tabular}](pic/g02_0407.gif)
Durch die beschränkte Auflösung der Maschinenzahlen kann es im ungünstigsten Fall zu einem sehr hohen Rundungsfehler kommen, der bewirkt, daß keine einzige Stelle im Ergebnis richtig ist.
Trotz der guten Kondition bezüglich Änderung der Integrandenfunktion ist anhand der verfügbaren diskreten Informationen auch in diesem Fall keine Aussage über den tatsächlichen Abstand der beiden Integrandenfunktionen möglich.
Es ist also unmöglich, eine exakte Fehlerabschätzung durchzuführen.
(Ein Ausnahme stellt die Transformation von unendlichen auf endliche Integrationsbereiche dar. Hier kann man durch Einführung einer Ableitungsschranke und durch eine geeignete Einschränkung der zulässigen Funktionen eine Genauigkeit r(S) (=Informationsradius ) bestimmen, doch eine derartige Einschränkung ist in den meisten Fällen nicht sinnvoll.)
[ < ]
[ globale Übersicht ]
[ Kapitelübersicht ]
[ Stichwortsuche ]
[ > ]
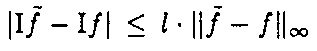
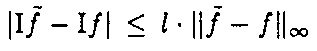
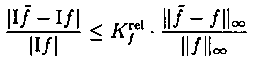
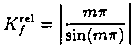
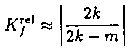

![\mbox{I}(f;[0,b]) := \int \limits_{0}^{b} (1-x)^{-0.9} \,dx =
-10 (1-b)^{0.1} + 10](pic/g02_0406.gif)
![\begin{tabular}{|l|llll|}
\hline
\strutHline
$ b $ & $1-10^{-5}$ & $1-10^{-10}$ & $1-10^{-15}$ & $1-10^{-20}$ \\
\hline
\strutNachHline
I$(f;[0,b])$ & 6.8377 & 9.0000 & 9.6838 & 9.9000 \\
\strutVorHline
$K_{0,b} = f(b)$ & $ 3.16 \cdot 10^{4} $ & $ 1.00 \cdot 10^{9} $ &
$ 3.16 \cdot 10^{13} $ & $ 1.00 \cdot 10^{18} $ \\
\hline
\end{tabular}](pic/g02_0407.gif)