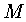 heißt ein metrischer Raum und ihre Elemente Punkte des Raumes,
wenn je zwei Elementen
heißt ein metrischer Raum und ihre Elemente Punkte des Raumes,
wenn je zwei Elementen
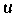 und
und
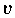 aus
aus
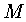 eine eindeutig bestimmte reelle Zahl
eine eindeutig bestimmte reelle Zahl
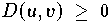 zugeordnet ist, die folgende Regeln erfüllt:
zugeordnet ist, die folgende Regeln erfüllt:
[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]
Definition: Metrischer Raum
Eine Menge
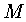 heißt ein metrischer Raum und ihre Elemente Punkte des Raumes,
wenn je zwei Elementen
heißt ein metrischer Raum und ihre Elemente Punkte des Raumes,
wenn je zwei Elementen
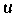 und
und
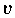 aus
aus
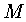 eine eindeutig bestimmte reelle Zahl
eine eindeutig bestimmte reelle Zahl
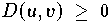 zugeordnet ist, die folgende Regeln erfüllt:
zugeordnet ist, die folgende Regeln erfüllt:
| 1. | 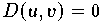 genau dann, wenn
genau dann, wenn
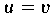
| (Definitheit),
| |
| 2. | 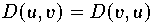
| (Symmetrie)
| |
| und | 3. | 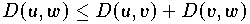
| (Dreiecksungleichung). |
Das Funktional
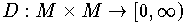
nennt man die Metrik
des Raumes; die Zahl
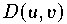 heißt die Distanz, der Abstand der Punkte
heißt die Distanz, der Abstand der Punkte
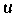 und
und
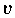 .
.
[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]