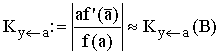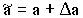[<] [globale Übersicht] [Kapitelübersicht] [Stichwortsuche] [>]


Konditionszahlen durch Differentation

Zur quantitativen Erfassung der auswirkungen von Änderungen wurden in der Mathematik die Differentialrechnung und der Abbleitungsbegriff eingeführt.

Sei f eine stetig differenzierbare Abbildung, die dem Datenwert a das Ergebnis y zuordnet: y = f(a).

Ändert man a in 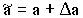$\tilde{a} = a + \Delta a$,

dann ändert sich y in: 

\[ \tilde{y} = f(\tilde{a}) = f(a + \Delta a) =
                 f(a) + f'(\overline{a}) \cdot \Delta a =
                 y + \Delta y; \]
\[ \Delta y = \tilde{y} - y = f'(\overline{a}) \cdot \Delta a. \]

was eigentlich dem Ergebnisänderung entspricht und
\[ \frac{\Delta y}{y} = \frac{a \cdot f'(\overline{a})}{f(a)} \cdot \frac{\Delta a}{a}. \]

relativen Änderungen.

Für hinreichend kleine Datenbereiche B erhält man damit:<IMG SRC=

[<] [globale Übersicht] [Kapitelübersicht] [Stichwortsuche] [>]