[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]

Matrizen mit allgemeiner Struktur

Kleine Einführung in die Materie

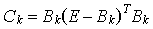
Wenn wir Matrizen mit allgemeiner Besetztheitsstruktur vorliegen haben, so können wir natürlich nur schwer vorhersagen, wo bei der Elimination neue Nicht-Null-Elemente entstehen werden. Man wird daher versuchen, die Auffüllung durch minimieren der lokalen Auffüllung zu reduzieren. Das so gewonnene Ergebnis ist zwar selten minimal (betrachtet auf die gesamteAuffüllung), aber wir werden doch oft eine deutliche Verringerung erreichen.

Man versucht nun die lokale Auffüllung zu ermitteln. Dabei gilt, daß die lokale Auffüllung beim kten Schritt von der Wahl des Pivotelements aus der Besetztheitsstruktur der noch nicht reduzierten unteren Hauptuntermatrix (d.h. der Matrix (n-k+1)x(n-k+1)) abhängt bzw. sich ermitteln läßt. Die dazu benötigte Besetztheitsstruktur wird durch eine Adjazenzmatrix wiedergegeben, die an jeder Position, an der in der ursprünglichen Matrix ein Nicht-Null-Element befand,nun den Wert "1" hat. Der Rest wird mit Nullen aufgefüllt.

Satz von der lokalen Auffüllung

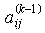Beim k-ten Eliminationsschritt des Gauß-Verfahrens und bei der Wahl des Elements $a_{ij}^{\left( k-1\right) }$ der Matrix 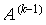$A^{\left( k-1\right) }$ als Pivotelement, ist die lokale Auffüllung gegeben durch das 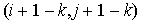$\left( i+1-k,j+1-k\right)$ -Element der Matrix
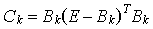
$C_k=B_k\left( E-B_k\right) ^TB_k$
wobei $B$ _k die Adjazenzmatrix der (n-k+1)x(n-k+1)-Hauptuntermatrix von $A$ ^(k-1) und E eine Matrix gleicher Dimension mit $c$ _ij=1 ist.
Nun kann man in jedem Schritt dasjenige Pivotelement auswählen, daß die geringste Auffüllung erzeugt.

In der Praxis wird dieses Verfahren allerdings kaum angewendet, da die Berechnung von $C$ _k viel zu aufwendig ist. Man begnügt sich daher meist mit einer Abschätzung der lokalen Auffüllung durch ermitteln der sogenannten Markowitz-Kosten.

Markowitz-Kosten

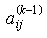Wird beim k-ten Schritt der Gauß-Elimination das Element $a_{ij}^{\left( k-1\right) }$ als Pivotelement gewählt, so sind die Markowitz-Kosten MK dieses Elements
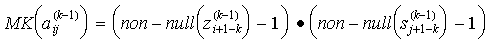
$MK\left( a_{ij}^{\left( k-1\right) }\right) =\left( non-null\left( z_{i+1-k}^{\left( k-1\right) }\right) -1\right) \bullet \left( non-null\left( s_{j+1-k}^{\left( k-1\right) }\right) -1\right)$

eine obere Schranke für die lokale Auffüllung. Dabei bezeichnet 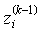$z_i^{\left( k-1\right) }$ die i-te Zeile und 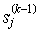$s_j^{\left( k-1\right) }$ die j-te Spalte der Matrix $B$ _k.
Wird das Pivotelement nun aber nur nach den Markowitz-Kosten ausgewählt, so verliert man eventuell wieder an numerischer Stabilität. Daher werden weitere Bedingungen aufgestellt, wie zB.

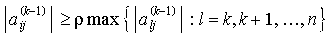
$\left| a_{ij}^{\left( k-1\right) }\right| \geq \rho \max \left\{ \left| a_{lj}^{\left( k-1\right) }\right| :l=k,k+1,\ldots ,n\right\}$

Diese Bedingung verhindert etwa ein zu starkes anwachsen von Rundungsfehlern (dabei muß allerdings $\rho \in \left( 0,1\right]$ passend gewählt werden).

Beispiel Adjazenzmatrix

Gegeben sei eine 5x5-Matrix:

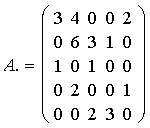
$A.=\left( \matrix 3 & 4 & 0 & 0 & 2 \\ 0 & 6 & 3 & 1 & 0 \\ 1 & 0 & 1 & 0 & 0 \\ 0 & 2 & 0 & 0 & 1 \\ 0 & 0 & 2 & 3 & 0\endmatrix \right)$

Die dazugehörige Adjazenzmatrix

B

₁ der nichtreduziertenMatrix A:

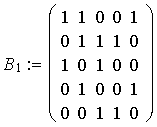
$B_1:=\left( \matrix 1 & 1 & 0 & 0 & 1 \\ 0 & 1 & 1 & 1 & 0 \\ 1 & 0 & 1 & 0 & 0 \\ 0 & 1 & 0 & 0 & 1 \\ 0 & 0 & 1 & 1 & 0\endmatrix \right)$

Nach Durchführung der ersten zwei Eliminationsschritte mit Spaltenpivotsuche erhalten wir die folgenden Adjazenzmatrizen:

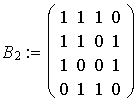
$B_2:=\left( \matrix 1 & 1 & 1 & 0 \\ 1 & 1 & 0 & 1 \\ 1 & 0 & 0 & 1 \\ 0 & 1 & 1 & 0\endmatrix \right)$

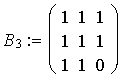
$B_3:=\left( \matrix 1 & 1 & 1 \\ 1 & 1 & 1 \\ 1 & 1 & 0\endmatrix \right)$

Beispiel Minimieren der lokalen Auffüllung

Für unsere Matrix berechnen wir

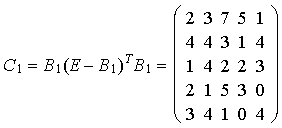
$C_1=B_1\left( E-B_1\right) ^TB_1=\left( \matrix 2 & 3 & 7 & 5 & 1 \\ 4 & 4 & 3 & 1 & 4 \\ 1 & 4 & 2 & 2 & 3 \\ 2 & 1 & 5 & 3 & 0 \\ 3 & 4 & 1 & 0 & 4\endmatrix \right)$

Nun könnten wir $a$ ₅₄ oder $a$ ₄₅ als Pivotelement wählen ( diese ergeben beide keine Auffüllung>. Wenn wir uns für $a$ ₅₄ entscheiden, so erhalten wir im nächsten Schritt

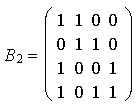
$B_2=\left( \matrix 1 & 1 & 0 & 0 \\ 0 & 1 & 1 & 0 \\ 1 & 0 & 0 & 1 \\ 1 & 0 & 1 & 1\endmatrix \right)$

Nach dem nächsten Eliminationsschritt haben wir dann

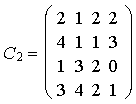
$C_2=\left( \matrix 2 & 1 & 2 & 2 \\ 4 & 1 & 1 & 3 \\ 1 & 3 & 2 & 0 \\ 3 & 4 & 2 & 1\endmatrix \right)$

und somit $a$ ₄₅⁽¹⁾ als Pivotelement keine Auffüllung ergibt.

[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]