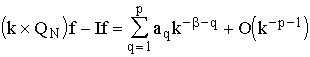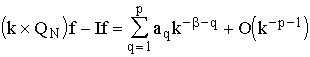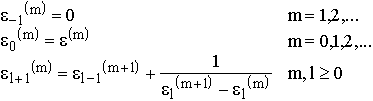[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]

Inhaltsverzeichnis Kapitel 7.4.6 Nichtlineare Extrapolation

  • 7.4.6.1 Allgemeines
  • 7.4.6.2 Epsilon-Algorithmus
  • Beispiel für den Epsilon-Algorithmus

    • 7.4.6 Nichtlineare Extrapolation

    7.4.6.1 Allgemeines:

    Die Euler-Maclaurinsche Summenformel kann hinsichtlich der Klasse von Integranden f, auf die sie angewendet werden kann, verallgemeinert werden. Wenn man z. B. f eine algebraische Endpunkt-Singularität besitzt,
    f(x) = xßh(x), -1 < ß <= 0, h aus Cp+1[a,b], dann gilt
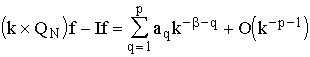
    $\left( k\times Q_N\right) f-If=\sum\limits_{q=1}^pa_qk^{-\beta -q}+O\left(k^{-p-1}\right) $

    Ähnliche - wenn auch kompliziertere - Entwicklungen erhält man für Integranden mit algebraisch-logarithmischen Endpunkt-Singularitäten und für Integranden mit inneren algebraischen Singularitäten. Man beachte, daß die (lineare) Richardson-Extrapolation nur dann zur Konvergenzbeschleunigung herangezogen werden kann, wenn der Exponent ß explizit bekannt ist. Wenn dies nicht der Fall ist, müssen nichtlineare Extrapolationsmethoden verwendet werden, um die Konvergenz von (k x QN)f zu beschleunigen.
    Für die Beschleunigung der Konvergenz sk = (k x QN)f --> If für k --> unendlich erweist sich - unter der Voraussetzung, daß die obige Formel zutrifft - die Shanks-Transformation als besonders geeignet.

    7.4.6.2 Epsilon-Algorithmus:

    Die Shanks-Transformation wird gewöhnlich in der Form des Epsilon-Algorithmus implementiert:
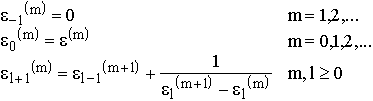
    $\matrix \epsilon _{-1}^{(m)}=0 & m=1,2,... \\ \epsilon _0^{(m)}=\epsilon^{(m)} & m=0,1,2,... \\ \epsilon _{l+1}^{(m)}=\epsilon _{l-1}^{(m+1)}+\frac1{\epsilon _l^{(m+1)}+\epsilon _l^{(m)}} & m,l\geq 0\endmatrix $

    Der Epsilon-Algorithmus ist - abgesehen von der Richardson-Extrapolation - das wichtigste Extrapolationsverfahren im Bereich der numerischen Integration. So beruhen z. B. alle Konvergenzbeschleunigungsverfahren des QUADPACK auf diesem Algorithmus.

    Beispiel (Epsilon-Altorithmus)
    Dieses Verfahren soll in Form eines interaktiven Beispiels gezeigt werden.

    [ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]