, den mathematisch "glattesten"
Funktionen, die beliebig oft differenzierbar sind:[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]
Ein Polygonzug gehört zur Klasse C0, d.h. zu jenen "nicht-glatten" Funktionen, die zwar stetig, aber nullmal, d.h. nicht differenzierbar sind. An den Knotenpunkten stimmen links- und rechtsseitige Ableitung eines Polygonzuges nicht überein.
Kubische Splinefunktionen (siehe Abschnitt 9.7) gehören zur Klasse C2: Die Funktionen selbst sowie ihre ersten und zweiten Ableitungen sind stetig, während die dritten Ableitungen Sprungstellen an den Knotenpunkten aufweisen.
Polynome (die nicht stückweise, sondern einheitlich definiert sind) gehören zur Klasse C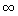, den mathematisch "glattesten"
Funktionen, die beliebig oft differenzierbar sind:
Die Planung der Bewegungsbahn (Trajektorie) eines Industrieroboters kann als "Bewegung von Punkt zu Punkt" erfolgen. Dabei wird die Trajetorie durch eine Reihe von Raumpunkten
Pi = (xi, yi, zi)T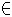 
R3, i = 1, 2, ..., k
definiert, die vom Effektor* zu vorgegebenen Zeitpunkten {ti} mit bestimmten Geschwindigkeiten {vi}zu durchlaufen sind.
Aus Tabellen von Bahnpunkten {Pi}müssen die Bahnen als Zeitfunktionen P(t) durch Interpolation bestimmt werden. Diese
Funktionen können zur Steuerung des Roboters oder z.B. zur Berechnung des Geschwindigkeits- und Beschleunigungsverlaufs
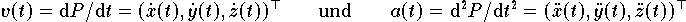
verwendet werden. Der Forderung nach einer "ruckfreien" Bewegung des Effektors entspricht die Forderung nach einer stetigen zweiten Ableitung (Beschleunigung) der Interpolationsfunktion (wodurch z.B. die Verbindung der Punkte {Pi} durch einen Polygonzug nicht in Frage kommt).
* Unter Effektoren versteht man Einrichtungen eines Industrieroboters, mit denen Manipulationen vorgenommen werden: mechanische Greifer, Schweißzangen, Farbspritzpistolen etc.
[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]