[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]

Verfahrensfehler

Mathematische Probleme, die nicht - oder nur mit unvertretbar hohem Aufwand - durch Formelmanipulation, rationale Rechenoperationen etc. lösbar sind, können nur mit numerischen Näherungsverfahren gelöst werden. Bei der Entwicklung derartiger Näherungsverfahren sind verschiedene Vereinfachungen notwendig, um die Finitisierung zu erreichen oder den Aufwand zu reduzieren.

Beispiel: (Eindimensionales Verschnittproblem) Die Teile Tn=(T1,T2,...,Tn) mit den Längen l(Ti) Î (0,1] sollen aus vorgegebenen Stücken B1, B2, ... der Länge 1 herausgeschnitten werden; jedes Ti aus einem Bj, sodaß die Anzahl L der erforderlichen B-Stücke minimal wird. Der Rechenaufwand aller bekannten Algorithmen zur exakten Lösung dieses Problems wächst (mindestens) exponentiell mit n. Dies hat zur Folge, daß bereits bei "mittelgroßen" Werten von n dieses Verschnittproblem auf heutigen Computern nicht mehr exakt gelöst werden kann, weil es viel zu lange dauern würde. Akzeptiert man hingegen als Ergebnis auch eine Näherung, die nur geringfügig größer als der optimale Wert ist, dann kann man dieses Problem mit erheblich geringerem Rechenaufwand (bis hinunter zu O(n log n)) ermitteln.

Abbruchfehler

Numerische Näherungsverfahren auf einem Computer können grundsätzlich nur aus einer endlichen Folge arithmetischer Rechenoperationen (Addition, Subtraktion, Multiplikation, Division) bestehen, wobei Anzahl und Abfolge der Rechenschritte im allgemeinen nicht a priori festliegen, sondern - abhängig von Daten und Zwischenergebnissen - im Verlauf der Berechnung durch Vergleiche,Abfragen etc. festgelegt werden. Auch in den vordefinierten Unterprogrammen für die elementaren Funktionen sin, cos, exp, ... wird rechnerintern nur eine endliche Folge arithmethischer Operationen ausgeführt.

Den Fehler, den man beim Abbruch eines unendlichen Prozesses begeht, bezeichnet man als Abbruchfehler (truncation error).

Beispiel: (Cosinus Funktion) Die mathematischen Standardfunktionen (Sinus-, Cosinus-, Eulersche e Funktion, etc) werden in der Analysis durch unendliche Reihen (Potenzreihen) definiert. Um zu Funktionsunterprogrammen für diese Funktion zu gelangen- wie sie als vordefinierte Unterprogramme Bestandteil der meisten Programmiersprachen sind- müssen die unendlichen Reihen durch endlche Ausdrücke - z.B. die Taylorpolynome, die man durch Abbruch der unendlichen Taylorreihen erhält- ersetzt werden.

Ersetzt man zum Beispiel die unendliche Reihe der Cosinus- Funktion

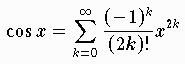
\cos{x}=\sum\frac{(-1)^k}{(2k)!}x^{2k}

durch

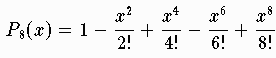
P_8(x)=1-\frac{x^2}{2!}+\frac{x^4}{4!}-\frac{x^6}{6!}+\frac{x^8}{8!}

so tritt ein Abbruchfehler

etrunc(x):=P8(x)-cos(x)

auf, der umso größer ist, je weiter x von 0 entfernt ist.

Diskretisierungsfehler

Den Fehler, den man durch das Ersetzen kontinuierlicher Information durch diskrete Information begeht, nennt man Diskretisierungsfehler. Es existiert also die Information für eine Funktion an jeder Stelle, da ein Computer jedoch nur endlich viele Zahlenwerte verarbeiten kann, begeht er einen Diskretisierungsfehler.

Beispiel:(Numerische Integration) Für die Ermittlung des Integralwertes eines Integrals über die Funktion f(t) liegt im Allgemeinen vollständige Information vor. Die Integrandenfunktion liegt also zum Beispiel als algebraischer Ausdruck vor, dessen Auswertung an beliebiger Stelle den Funktionswert liefert. Da in einem Computerprogramm jedoch nur endlich viele Werte berücksichtigt werden können, werden von der im Prinzip zwar vorhandenen, aber numerisch nicht nutzbaren kontinuierlichen Information nur endlich viele diskrete Punkte zur Berechnung herangezogen, wodurch ein Diskretisierungsfehler entsteht.

Verfahrensfehler (effekte)

Alle bei der Konstruktion eines numerischen Verfahrens (Algorithmus) gemachten Vereinfachungen werden als Verfahrensfehler und ihre Auswirkungen auf das gesuchte Resultat als Verfahrensfehlereffekt bezeichnet. Der Verfahrensfehlereffekt ist die Abweichung der (durch rundungsfehlerfreie Berechnungen gewonnenen) Näherungslösung von der „exakten" Lösung des mathematischen Problems.

Terminologie (Verfahrensfehler) In der Numerischen Mathematik ist meist folgende Bezeichnungsweise gebräuchlich: Jene Größe, die soeben als Verfahrensfehlereffekt bezeichnet wurde, wird kurz als Verfahrensfehler bezeichnet. Für Verfahrensfehler im obigen Sinn gibt es in der Literatur im allgemeinen keine spezielle Bezeichnung.

Im folgenden wird der übliche Sprachgebrauch übernommen, d.h., die Bezeichnung „Verfahrensfehler" wird anstelle des „Verfahrensfehlereffekts" verwendet.

Reduktion des Verfahrensfehlers

In den meisten Fällen kann der Verfahrensfehler durch Erhöhung des Aufwandes beliebig verkleinert werden. Man spricht dann von konvergenten Näherungsverfahren. Durch den bei praktischen Berechnungen stets erforderlichen Abbruch nach endlich vielen Berechnungsschritten ist der Verfahrensfehler unvermeidlich.

Beispiel: Wenn man die unendliche Summe von 1+1/2+..+1/n berechnen will, und der Computer nur n=2 Schritte berechnet, dann ist das Ergebnis ungenauer, als wenn er bis n=10000 rechnet. Durch Erhöhung des Aufwandes wird die Rechengenauigkeit erhöht.

Schranken für den Verfahrensfehler

Bei vielen Näherungsverfahren können Fehlerschranken hergeleitet werden, die es im Prinzip gestatten, in einem konkreten Anwendungsfall ein bestimmtes Verfahrensfehlerniveau zu garantieren.

Vorraussetzung für die Anwendbarkeit von Verfahrensfehlerschranken ist oft die explizite (zahlenmäßige) Kenntnis bestimmter problemcharakterisierender Größen. Da diese Größen oft nicht bekannt sind oder nur mit unzumutbar hohem Aufwand ermittelt werden können, werden derartige Fehlerschranken für quantitative Fehlerschätzungen in der Praxis nur selten eingesetzt . Trotzdem spielen detailierte Aussagen über Verfahrensfehler eine wichtige Rolle bei der qualitativen Beurteilung bzw. Bewertung numerischer Näherungsverfahren, da sie Aussagen über deren Effizienz hinsichtlich ganzer Problemklassen gestatten.

Um die Einhaltung vorgegebener Toleranzen in praktischen Situationen überprüfen zu können, sind meist Abschätzungen des tatsächlichen Verfahrensfehlers erforderlich. In den meisten numerischen Anwendungen wird mit a-posteriori-Fehlerschätzungen gearbeitet. Dabei wird der Verfahrensfehler auf Grund von Informationen geschätzt, die man erst während des Rechenverlaufs erhält. Diese Art der Fehlerschätzung gestattet es in vielen Fällen nicht, Fehlerschranken zu garantieren, liefert jedoch für große Problemklassen mit hoher Wahrscheinlichkeit ausreichend genaue Hinweise auf das tatsächliche Fehlerniveau.

[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]