[<] [globale Übersicht] [Kapitelübersicht] [Stichwortsuche] [>]

Fallstudie : Quadratische Gleichung

Durch die quadratische Gleichung y2+a1y+a0=0 werden im Fall a21-4a0>0 den beiden Datengrößen a0 und a1, die beiden Ergebnisgrößen y1 und y2 zugeordnet:

\begin{eqnarray*} y_1 & = & ( \sqrt{a_{1}^{2} - 4a_{0}} - a_{1})/2, \\ y_2 & = & (-\sqrt{a_{1}^{2} - 4a_{0}} - a_{1})/2. \end{eqnarray*}

Zur Bestimmung der relativen Konditionszahlen

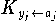
$K_{y_{j} \gets a_i}$

muß man die partiellen Abbildungen

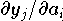
$\partial y_{j} / \partial a_{i}$

bilden:

\[ \frac{\partial y_j}{\partial a_1} = \frac{1}{2} \left( \pm \frac{a_1}{\sqrt{a_{1}^{2} - 4a_0}} - 1 \right) = \frac{\pm a_1 - \sqrt{a_{1}^{2} - 4a_0}}% {2 \sqrt{a_{1}^{2} - 4a_0}} \, , \]

\[ \frac{\partial y_1}{\partial a_1} = -\frac{y_1}{\sqrt{a_{1}^{2} - 4a_0}}, \qquad \frac{\partial y_2}{\partial a_1} = \frac{y_2}{\sqrt{a_{1}^{2} - 4a_0}}. \]

Analog erhält man:
\[ \frac{\partial y_1}{\partial a_0} = -\frac{1}{\sqrt{a_{1}^{2} - 4a_0}}, \qquad \frac{\partial y_2}{\partial a_0} = \frac{1}{\sqrt{a_{1}^{2} - 4a_0}}. \]
Die Konditionszahlen

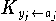
$K_{y_{j} \gets a_i}$

sind daher nach ( 2.28 )
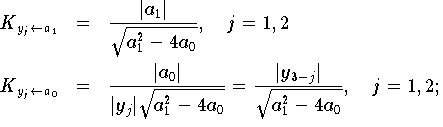
\begin{eqnarray} K_{y_{j} \gets a_1} & = & \frac{|a_{1}|}{\sqrt{a_{1}^{2} - 4a_0}}, \quad j = 1, 2 \label{eqn:kond7a} \\ K_{y_{j} \gets a_0} & = & \frac{|a_{0}|}{|y_j| \sqrt{a_{1}^{2} - 4a_0} } = \frac{|y_{3-j}|}{\sqrt{a_{1}^{2} - 4a_0} }, \quad j = 1, 2; \label{eqn:kond7b} \end{eqnarray}
bei der letzten Umformung wurde y1.y2=a0 werwendet. Beschränkt man sich z.B. auf den Fall a0< 0, so ist \[ |y_{j}| < \sqrt{a_{1}^{2} - 4 a_0} \qquad \mbox{und} \qquad |a_{1}| < \sqrt{a_{1}^{2} - 4 a_0}; \]

und damit sind alle vier Konditionszahlen kleiner als eins!(gut konditioniert).

Zahlenbeispiel: a1 = 5 a0 = - 0.1 => y1 = 5.01992... y2 = -0.0199206...

Eine Änderung der Daten um 2% : a1 = -4.9 und a0 = -0.098 ändert die Lösung in : y1 = 4.91932... y2 = -0.019919... d.h. ebenfalls um 2% bei y1 und nur um weniger als 0.01% bei y2 !!!


[<] [globale Übersicht] [Kapitelübersicht] [Stichwortsuche] [>]