9. Schwach besetzte lineare Systeme

Im vorhergehenden Kapitel wurde ausführlich die Lösung linearer Gleichungssysteme mit voll (bzw. relativ dicht) besetzten Matrizen besprochen. Hier werden nun Lösungsverfahren für schwach besetzte Matrizen vorgestellt.

Was ist nun eine schwach besetzte Matrix? Nun, die Antwort dürfte nicht wirklich schwer fallen. Es handelt sich dabei um lineare Systeme der Gestalt A x = b, bei denen der Großteil der Koeffizienten der Matrix A gleich Null ist.

Der etwas voreilige Leser könnte nun einwenden:

1. Solche Systeme treten in der Praxis nur selten auf.
2. Und sollten sie wirklich einmal auftauchen, es sind ja trotz allem lineare Gleichungssysteme. Verwendet man einfach die bisher vorgestellten Algorithmen.

Die Frage ist also, wann erhält man schwach besetzte Systeme. Zum Beispiel überall dort, wo partielle Differentialgleichungen (ich weiß, diese Worte lösen einen kalten Angstschweiß aus, aber keine Sorge, es wird "trivial") numerisch gelöst werden.

Gehen wir die Sache ganz langsam an. Dem Computer beizubringen, eine beliebige Funktion zu differenzieren, ist zwar nicht prinzipiell unmöglich, ist aber sicherlich ein "kniffliges" Problem und stellt hohe Anforderungen an den Programmierer. Doch oft ist dieser große Aufwand gar nicht notwendig, man kann Ableitungen ja auch schätzen.

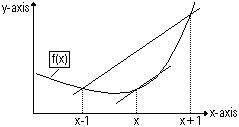
Den 2-dimensionalen Fall sollte wirklich jeder aus der Schule kennen. Man hat eine Funktion y = f(x) gegeben und möchte die Steigung in einem bestimmten Punkt f(x) schätzen. Man geht also her und berechnet f(x-1) und f(x+1), verbindet diese beiden Punkte und - voila - man hat eine Näherung (z.T. eine relativ schlechte, wenn man das Beispiel unten betrachtet) für die Steigung im Punkt f(x). Diese Schätzung kann beliebig genau werden, da man die Abstände zwischen den Punkten auf der x-Achse immer kleiner machen kann.

Das war doch nun wirklich nicht schwer, oder? Dann gehen wir gleich einen Schritt weiter. Hat man nun eine Funktion z = f(x, y), also eine 3-dimensionale Funktion, so muß zunächst die Grundfläche (die Ebene, die durch die x- und y-Achse aufgespannt wird) diskretisiert werden. D.h., es werden nicht alle Punkte der Ebene betrachtet, sondern nur vorher ausgewählte (siehe 2-dim. Fall: es wird nicht die gesamte Funktion betrachtet, sondern nur die Punkte ..., x-1, x, x+1, ...). Normalerweise wird, um die Berechnungen einfach zu halten, ein rechteckiger Bereich gewählt, der mit einem regelmäßigen Netz aus Gitterpunkten überspannt wird.
Nun kann die Steigung an einem beliebigen Gitterpunkt (Randpunkte müssen gesondert behandelt werden) ähnlich wie im 2-dim. Fall geschätzt werden. Nur hat man hier das zusätzliche Problem, daß die Steigung in einem bestimmten Punkt f(x, y) nicht ein einziger Wert ist (legt man einen Schnitt durch die Funktion einmal in x-, dann in y-Richtung, so ist einzusehen, daß die beiden dabei beobachteten Steigungen nicht unbedingt gleich sein müssen). Theoretisch würde es unendlich viele Steigungen in einem Punkt geben. Aber man hat ja die Grundfläche bereits diskretisiert, d.h. es ist sowieso unmöglich, eine Steigung in beliebiger Richtung anzunähern (um ein z.B. physikalisches Modell überhaupt berechenbar zu machen, muß es meist vereinfacht werden [z.B. durch Diskretisierung], damit gehen aber natürlich Informationen verloren). Man verwendet daher meist alle zur Verfügung stehenden Nachbarpunkte in einer sog. 8-Nachbarschaft.

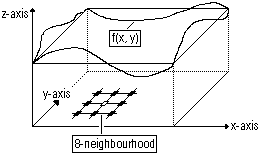
Um also die Steigungen in einem gewählten Punkt zu schätzen, werden 9 Werte benötigt: der Punkt selbst und seine 8 Nachbarn; Randpunkten stehen natürlich je nach Position weniger Nachbarn zur Verfügung. Sei nun n die Anzahl der Gitterpunkte, so kann man eine Matrix mit den Dimensionen n x n aufbauen, wobei jede Zeile bzw. jede Spalte einem bestimmten Gitterpunkt entspricht. Trägt man nun für jeden Punkt die entsprechenden Werte, die für die Steigungsberechnung benötigt werden, ein, so erhält man bei methodischem Vorgehen (die rechteckige Grundfläche zeilenweise von z.B. links oben nach rechts unten durcharbeiten) eine Matrix mit folgender Gestalt:

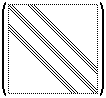
Was hat man nun damit erreicht? Nun, das Wichtigste ist sicher, daß das ursprüngliche Problem, die Lösung einer partiellen Differentialgleichung, auf ein einfacher lösbares, nämlich die Berechnung eines linearen Gleichungssystems, abgebildet wurde. Wie aber leicht erkennbar ist, besteht die gebildete Matrix fast nur aus Nullen, da in jeder Spalte und Zeile maximal 9 Nichtnullelemente vorkommen, die Anzahl der Gitterpunkte n aber fast beliebig groß werden kann (kommt auf die Genauigkeit bzw. die Dimension [z.B. 3-dim. + Zeit als vierte Dimension, ...] des Modells an).

Die Matrix aus dem obigen Beispiel hat eine regelmäßige Bandstruktur. Man kann sich aber leicht vorstellen, daß diese immer mehr "gestört" wird, wenn die Grundfläche kein Rechteck mehr ist, die Gitterstruktur unregelmäßig ist, mehr Nachbarpunkte in die Steigungsberechnung einfließen oder, bei 4-dim. oder höherdimensionalen Problemen, die Grundfläche zu einem "Grundkörper" mit beliebiger Struktur wird (siehe Matrizentypen).
Für die Berechnung von z.B. Autokarosserieverformungen wird heute die Finite-Elemente-Methode verwendet. Die Nachbarschaftsbeziehungen zwischen den einzelnen Elementen (nichts anderes wird ja in der Matrix abgespeichert) sind dabei so "wirr", daß die Matrix zwar weiterhin sehr schwach besetzt ist, über die Struktur derselben kann aber überhaupt nichts mehr ausgesagt werden (wird der rechte vordere Kotflügel verbogen, hat das nun mal keine direkte Auswirkung auf den Kofferraumdeckel; eine Kraftübertragung wird nur durch die Elemente dazwischen ermöglicht).

Die Standardalgorithmen zur Lösung lin. Gleichungssysteme, wie sie in Kapitel 8 vorgestellt wurden, sind für Berechnungen mit schwach besetzten Matrizen nur bedingt geeignet, und zwar aus folgenden Gründen:

1. Der Speicheraufwand von O(n²) ist für schwach besetzte Matrizen nicht notwendig; es genügt, die Elemente ungleich Null abzuspeichern. Diesem Punkt kommt deshalb eine so große Bedeutung zu, da die Dimensionen bei dieser Art von Matrizen meist deutlich größer sind (z.B. n=100.000) als bei voll besetzten Systemen.
2. Die Algorithmen sind ineffizient, da z.B. bei den Matrix-Vektorprodukten viele Teile durch Multiplikation mit Null verschwinden (Aufwand normalerweise bei O(n³) kann deutlich gedrückt werden).

Dieses Kapitel beschäftigt sich also im weiteren mit speziellen Speicherformaten für schwach besetzte Matrizen und vor allem mit Algorithmen, die z.T. Spezialisierungen der in Kapitel 8 behandelten sind. Diese Spezialisierungen sind notwendig, da man zusätzlich noch mit 2 neuen Problemen bei dieser Klasse von Matrizen konfrontiert ist: das "fill-in" (Erzeugung neuer Nichtnullelemente während des Verfahrens) muß gering gehalten werden und die algorithmische Effizienzsteigerung hat meist eine numerische Destabilisierung zur Folge. Eine ausbalancierte Verfolgung der verschiedenen Ziele ist Grundvoraussetzung für die Verwendbarkeit der verschiedenen Algorithmen.

Hier nun noch eine kurze Liste von möglichen Erscheinungsbildern schwach besetzter Matrizen. Diese Liste erhebt natürlich keinen Anspruch auf Vollständigkeit.
Die weißen Flächen in der Grafik stehen für Nullen.

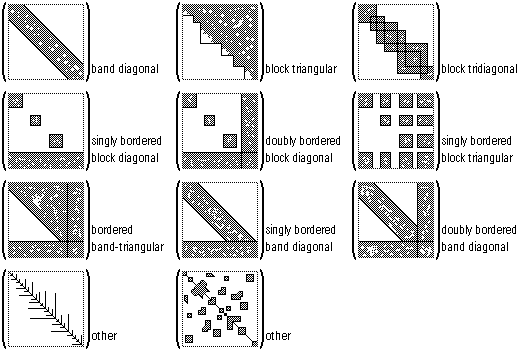
Die deutschen Bezeichnungen der einzelnen Matrizen sind direkt ableitbar.