Das folgende Kapitel ist unmittelbar mit 5.4 Schleifentransformation verbunden. Es soll hier der Inhalt hier an konkreten Beispielen anschaulich gemacht werden.
In diesem Kapitel geht es ausschließlich um Optimierungen der Laufzeit. Jene von Compilezeiten und Programmgröße bleibt hier außen vor. Zunächst befassen wir uns mit Dingen die für das Verständnis nötig sind.
"Cache as Cash can."
Zu diesem Punkt, siehe auch ein bißchen
5.2 Ursachen geringer Effizienz.
Die Prozessoren sind um vieles schneller als Speicher. Um dieses Manko zu
mildern, versucht man jene Informationen die häufiger benötigt
werden,
in einem schnelleren und teueren Zwischenspeicher (= Cache) zu
halten.
Greift der Prozessor nun auf Daten zu, die im Cache liegen
(= Cache Hit), dann werden diese in sehr kurzer Zeit geliefert;
nur wenn die die angeforderten Daten nicht im Cache sind
(= Cache Miss), muß auf den langsameren Speicher zugegriffen
werden.
Das Problem besteht darin eine Strategie zu finden, damit jene Speichereinheiten, die als Nächstes gebraucht werden, sich im Cache befinden.
Hierbei kommt einem die Tatsache das sich Speicherzugriffe innerhalb eines gewissen Bereiches wiederholen, zu Gute. D.h. ein Programm greift nicht mit gleicher Wahrscheinlichkeit auf all seinen Code zu (Prinzip der Lokalität). Da sind zwei verschiedene Arten von Lokalität:
Lokalität in Programmen treten aufgrund von einfachen und natürlichen Programmstrukturen auf.
| Beispiel | Lokalität |
|---|---|
|
Temporal |
|
Spatial |
|
Spatial |
Die Idee der Programmoptimierung: Jene Operationen bei denen dieses Schema der Lokalitat nicht gilt, so zu verändern daß auch diese vom Zwischenspeicher profitieren.
Diese Speicherhierachie ist die Grundlage aller hier vorgestellten Geschwindigkeitsverbesserungen. Somit wäre bei Einführung einer neuen Technologie, die zuerst im Speicherbereich umgesetzt werden würde, alles hier gesagte über Jahrzehnte hinweg belanglos.
Zweidimensionales Array: So existieren bei der Angabe der Indizes beide Konventionen, sowohl in der Reihenfolge wie in der Mathematik üblich, als auch andersrum. Ebenso verschieden ist die Abbildung auf die Speicheraddressen.
Darstellung einer Matrix mit 2 Zeilen und 5 Spalten:
Speicherbelegung:
(1)(2)(3)(4)(5) (1)(2)(3)(4)(5)
[(1)(2)(3)(4)(5)] [(1)(2)(3)(4)(5)]
Zugehöhrige Definitionen
(h3):| Sprache | Variablendefinition | Verwendug |
|---|---|---|
| FORTRAN (p1) | REAL, DIMENSION (2,5) :: mat (a1) | mat(1,4) |
| C & C++ (p2) | double mat[5][2]; | mat[3][0] |
| Pascal | VAR mat: ARRAY[1..2, 1..5] OF REAL; | mat[1,4] |
| PL/I | DCL mat(2, 5) BINARY FLOAT; | mat(1,4) |
Common Subexpression Elimination: Das "common subexpression elimination"-Modul erkennt Ausdrücke die mehr als einmal auftreten und das selbe Ergebnis bringen; berechnet das Ergebnis, und ersetzt jedes Vorkommen des Ausdrucks damit. Die Möglichkeiten des Teilausdrucks umspannen Befehle die Werte aus dem Speicher laden, ebenso gut wie arithmetische Berechnungen. Zum Beispiel, der Quelltext
A = X + Y + Z
B = X + Y + W
wird zu
T1 = X + Y
A = T1 + Z
B = T1 + W
Loop Invariant Code Motion: Das "loop invariant code motion"-Modul erkennt Befehle innerhalb einer Schleife dessen Werte sich nicht ändern, und plaziert diese außerhalb der Schleife. Zum Beispiel, der Quelltext
X = Z
DO I = 1,10
A(I) = 4 * X + I
END DO
wird zu
X = Z
T1 = 4 * X
DO I = 1,10
A(I) = T1 + I
END DO
Diese hier vorgestellten Optimierungen werden im folgenden als vorhanden angenommen. Eine vertiefende Darstellung dieser, wird anhand von später verwendeten Quelltexten veranschaulicht. Darüber hinaus, gibt es sehr viele weitere Möglichkeiten die sich zur Optimierung eignen.
| Verschiedene weitere Quelltexte zur Veranschaulichung |
In vielen Fällen müssen Sie aber den Compiler unterstützen, z.B. um klarzustellen, ob die Laufzeit oder der Speicherverbrauch wichtiger sind. Lesen Sie die allgemeinen, nicht speziell numerischen Hinweise zur Optimierung von FORTRAN-Quelltext, wenn Sie Ihrem FORTRAN-Compiler etwas entgegenkommen wollen.
Auf weitergehende automatische Optimierungen speziell für die numerische Mathematik wird später unter Präcompiler und Optimierer noch eingegangen.
Die vorgenommenen Leistungsmessungen erfolgten auf einer HP-Workstation. Reproduzierbar sind die Resultate nur auf völlig gleichartigen Systemen. Man kann sie jedoch qualitativ auf andere Systeme übertragen.
Man vertausche innere und äußere Schleifen(-indizes) so, das weiterhin das selbe (etwas schneller) berechnet wird.
Beispiel: Multiplikation
(h1)
von 2 quadratischen
(h2)
Matrizen
Bei vielen Matrizenoperationen ist das errechnete Ergebnis
nicht, von
der Reihenfolge in welcher die Matrixelemente bearbeitet werden,
abhängig.
REAL, DIMENSION (qmax, qmax) :: a, b, c
c = 0
DO i = 1, qmax, 1
DO j = 1, qmax, 1
DO k = 1, qmax, 1
c(i,j) = c(i,j) + a(i,k)*b(k,j)
END DO
END DO
END DO
Dieser Algorithmus erfordert qmax3 Gleitpunktmultiplikationen.
Weiters werden ebensoviele Additionen benötigt.
Verfahren mit niedrigerer Komplexität finden Sie unter
4.5 Komplexität von Algorithmen
und im Buch
| Schleifen- | Funktion | innere Schrittweite | ||||
|---|---|---|---|---|---|---|
| anordnung | innerste | mittlere | äußere | a | b | c |
| ijk | SDOT | SCPY | - | qmax | 1 | - |
| jik | SDOT | SCPY | - | qmax | 1 | - |
| kij | SAXPY | - | - | - | qmax | qmax |
| ikj | SAXPY | - | - | - | qmax | qmax |
| jki | SAXPY | - | - | 1 | - | 1 |
| kji | SAXPY | - | - | 1 | - | 1 |
Da die Charakteristika im wesentlichen durch die innerste Schleife bestimmt werden, unterscheiden sich die Algorithmusvarianten mit demselben innersten Laufvariablen in ihrem Leistungsverhalten nur minimal. Die nachfolgende Abbildung enthält daher nur drei Varianten.
Bei der ijk-Variante ist die Anzahl der Cache-Schreibzugriffe
im Verhältnis zu den Gleitpunktoperationen am geringsten,
während dieses Verhältnis
bei den anderen Beiden deutlich ungünstiger ist.
ijk ... 1 Schreibzugriff bei 2*qmax flop
jki ... qmax Schreibzugriffe bei 2*qmax flop
kij ... detto
Dies ist insoferne wichtig, da Schreibzugriffe meist eine längere
Ausführungszeit benötigen.
| Bei dem getesteten Rechner: | 1,5 Zyklen für Schreiben, gegenüber |
| 1 Zyklus beim Lesen und Gleitpunktrechnen |
Auf Grund ihrer hohen Referenzlokalität ist aber die jki-Variante den beiden anderen eindeutig überlegen.
Für Matrixgrößen über 300 ist ein deutlicher Leistungseinbruch bei allen Varianten feststellbar (mehr Cache-Fehlzugriffe). Hierfür der Grund ist, daß die laufend benötigten Teile der drei Matrizen nicht mehr vollständig im Cache gehalten werden können.
Man dupliziere den zu wiederholenden Teil und passt die Schleife
entsprechend an. Dadurch kann man sich einerseits Rechenschritte
sparen, z.B. die Prüfung der Schleifenbedingung erfolgt nur jedes
n-te Mal. Weiters ist eine Parallelisierung dadurch vielfach möglich.
Die Pipeline des Prozessors kommt dadurch auch stärker zum tragen.
REAL, DIMENSION (qmax, qmax) :: a, b, c
c = 0
DO i = 1, qmax, 4 ! Aufrolltiefe: 4 (= dreifach aufgerollt)
DO k = 1, qmax, 4 ! Aufrolltiefe: 4
DO j = 1, qmax, 1
c(i ,j) = c(i ,j) + a(i ,k )*b(k ,j)
c(i ,j) = c(i ,j) + a(i ,k+1)*b(k+1,j)
c(i ,j) = c(i ,j) + a(i ,k+2)*b(k+2,j)
c(i ,j) = c(i ,j) + a(i ,k+3)*b(k+3,j)
c(i+1,j) = c(i+1,j) + a(i+1,k )*b(k ,j)
c(i+1,j) = c(i+1,j) + a(i+1,k+1)*b(k+1,j)
c(i+1,j) = c(i+1,j) + a(i+1,k+2)*b(k+2,j)
c(i+1,j) = c(i+1,j) + a(i+1,k+3)*b(k+3,j)
c(i+2,j) = c(i+2,j) + a(i+2,k )*b(k ,j)
c(i+2,j) = c(i+2,j) + a(i+2,k+1)*b(k+1,j)
c(i+2,j) = c(i+2,j) + a(i+2,k+2)*b(k+2,j)
c(i+2,j) = c(i+2,j) + a(i+2,k+3)*b(k+3,j)
c(i+3,j) = c(i+3,j) + a(i+3,k )*b(k ,j)
c(i+3,j) = c(i+3,j) + a(i+3,k+1)*b(k+1,j)
c(i+3,j) = c(i+3,j) + a(i+3,k+2)*b(k+2,j)
c(i+3,j) = c(i+3,j) + a(i+3,k+3)*b(k+3,j)
END DO
END DO
END DO
Die äußeren beiden Schleifen wurden je 3-fach aufgerollt, deswegen
stehen 16 Anweisungen im Schleifenrumpf statt einer.
Durch das Aufrollen der Schleifen wird:
Leistungsvergleich zwischen:
Dieses bessere Leistungsverhalten der weniger stark aufgerollten Variante bei kleinen Matrizen, kommt durch die bessere Nutzung der Register zustande. Es werden ca. 30 Gleitpunktregister für Matrixelemente gegenüber von ca. 100 bei 7-fachen Schleifenaufrollen.
Da auf der verwendeten HP-Workstation nur 64 Gleitpunkt-Register zur Verfügung stehen, kann sich die Leistungsminderung durch Register-Umbelegungen bei der 7-fach-Aufroll-Version auswirken.
| Matrizen | kleine | große |
|---|---|---|
| im Cache | können im Cache gespeichert werden | passen nicht mehr in den Cache |
| günstiger | 3-faches Aufrollen | 7-faches Aufrollen |
| Ursache | bessere Registerausnutzung | höhere Referenzlokalität |
Bei Matrizen die nicht völlig in den Cache (n>200) bzw. in den Hauptspeicher passen (n>1600), brechen alle ikj-Varianten sehr stark ein. Hier zeigen die nun folgend gezeigten jki-Varianten weit besseres Verhalten.
REAL, DIMENSION (qmax, qmax) :: a, b, c
c = 0
DO j = 1, qmax, 4 ! Aufrolltiefe: 4 (= dreifach aufgerollt)
DO k = 1, qmax, 4 ! Aufrolltiefe: 4
DO i = 1, qmax, 1
c(i,j ) = c(i,j ) + a(i,k )*b(k ,j )
c(i,j ) = c(i,j ) + a(i,k+1)*b(k+1,j )
c(i,j ) = c(i,j ) + a(i,k+2)*b(k+2,j )
c(i,j ) = c(i,j ) + a(i,k+3)*b(k+3,j )
c(i,j+1) = c(i,j+1) + a(i,k )*b(k ,j+1)
c(i,j+1) = c(i,j+1) + a(i,k+1)*b(k+1,j+1)
c(i,j+1) = c(i,j+1) + a(i,k+2)*b(k+2,j+1)
c(i,j+1) = c(i,j+1) + a(i,k+3)*b(k+3,j+1)
c(i,j+2) = c(i,j+2) + a(i,k )*b(k ,j+2)
c(i,j+2) = c(i,j+2) + a(i,k+1)*b(k+1,j+2)
c(i,j+2) = c(i,j+2) + a(i,k+2)*b(k+2,j+2)
c(i,j+2) = c(i,j+2) + a(i,k+3)*b(k+3,j+2)
c(i,j+3) = c(i,j+3) + a(i,k )*b(k ,j+3)
c(i,j+3) = c(i,j+3) + a(i,k+1)*b(k+1,j+3)
c(i,j+3) = c(i,j+3) + a(i,k+2)*b(k+2,j+3)
c(i,j+3) = c(i,j+3) + a(i,k+3)*b(k+3,j+3)
END DO
END DO
END DO
Hier sind kaum Leistungseinbußen bei sehr großen Matrizen festzustellen.
Schleifenaufrollen muß nicht in jeden Fall eine Verbesserung bringen.
Die durch 3-faches Aufrollen der innersten Schleife entstehende
Jedes Element der ursprünglichen Matrix fällt genau in eine
Untermatrix (auch Block).
Der allgemeine Fall wird in
Zur einfacheren und lesbareren Darstellung wird im folgenden angenommen,
daß die Matrizen in quadratische Untermatrizen zerlegt werden.
Mit nb=n/b und
mb=m/b;
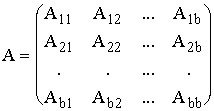
Die Zerlegung von A hat dann die Gestalt:


Will man einen Matrix-Algorithmus so umformen, daß eine bestimmte Ebene der Speicherhierachie gut ausgenutzt wird, so formuliert man diesen als Blockalgorithmus. Die Größe der Teilmatrizen ist dann so zu wählen, daß einerseits sämtliche beteiligeten Operandenblöcke in der betreffenden Speicherebene Platz finden, und andererseits die Anzahl der mit den Elementen dieser Blöcke ausgeführten Operationen maximal wird.
Hierfür kann eine der sechs Multiplikationsversionen
angewendet werden, z.B.:
REAL, DIMENSION (qmax, qmax) :: a, b, c
c = 0
DO ii = 1, qmax, nb
DO kk = 1, qmax, nb
DO jj = 1, qmax, nb
Cii,jj := Cii,jj + Aii,kk.Bkk,jj
END DO
END DO
END DO
Für die Multiolikation Aii,kk.Bkk,jj kann
davon unabhängig eine andere der sechs Varianten gewählt werden.
Es gibt daher 36 geblockte Versionen der Matrizenmultiplikation.
Bei der Multiplikation von Blockmatrizen zeigt sich, daß die Anordnung der zwei äußeren Schleifen auf das Leistungsverhalten unerheblich ist. Dieses wird, wie bei den ungeblockten Varianten, im wesentlichen durch die innerste Schleife bestimmt.
REAL, DIMENSION (qmax, qmax) :: a, b, c
c = 0
DO ii = 1, qmax, nb
DO kk = 1, qmax, nb
DO jj = 1, qmax, nb
DO j = jj, MIN(qmax, jj+nb-1)
DO k = kk, MIN(qmax, kk+nb-1)
DO i = ii, MIN(qmax, ii+nb-1)
c(i,j) = c(i,j) + a(i,k)*b(k,j)
END DO
END DO
END DO
END DO
END DO
END DO
Die Leistungsdaten, die der nachfolgenden Abbildung zugrundeliegen, wurden
mit der Blockgröße nb=128 ermittelt. Dieser Wert wurde der
verwendeten Workstation angepasst und entspricht einem sehr flachen
Optimum. Andere Blockungsfaktoren, im Bereich zwischen 80 und 256, liefern
fast genauso gute Resultate.
Daten werden in Hilfsfelder umkopiert. Diese nehmen jeweils einen Block
(eine Teilmatrix von A, B oder C) auf.
Idee: Alle Berechnungen werden mit den Hilfsfeldern
durchgeführt, sodaß keine Cache-Konflikte auftreten und die
Schrittweite beim Zugriff auf keinen Fall größer als die
Zeilenzahl nb des Blocks ist. Ohne diese Hilfsfelder können
bei geblockten Multiplikationsalgorithmen die Zugriffs-Schrittweiten im
ungünstigsten Fall n sein.
Weiters kann bei der Verwendung von Hilfsfeldern der zu bearbeitende Block transponiert (h4) kopiert werden. Damit kann man bei den innersten Schleifen alle Zugriffsschrittweiten kleinstmöglich halten.
Das Kopieren eines Blockes bietet sich vor allem für die Matrix A an. Dadurch wird auch für die ijk-Variante - die sich durch eine geringe Zahl von Schreibzugriffen auszeichnet - eine sehr gute Datenlokalität erreicht.
REAL, DIMENSION (qmax, qmax) :: a, b, c
REAL aa(nb, nb) ! Hilfsfeld
c = 0
DO ii = 1, qmax, nb
DO kk = 1, qmax, nb
DO jj = 1, qmax, nb
DO ib = ii, MIN(qmax, ii+nb-1)
aa(kb-kk+1,ib-ii+1) = a(ib,kb) ! Kopieren und Transponieren
END DO
END DO
DO jj = 1, qmax, nb
DO j = jj, MIN(qmax, jj+nb-1)
DO k = kk, MIN(qmax, kk+nb-1)
DO i = ii, MIN(qmax, ii+nb-1)
c(i,j) = c(i,j) + aa(k-kk+1,i-ii+1)*b(k,j)
END DO
END DO
END DO
END DO
END DO
END DO
Für die ikj-ijk-Variante ergibt sich für
größere Matrizen (m>700) eine wesentliche Leistungssteigerung.
Da die Elemente von A nun spalten- statt zeilenweise
dereferenziert werden. Bei den anderen Versionen sind dagegen kaum
Leistungssteigerungen feststellbar. Die folgend dargestellten Kurven wurden
wieder mit der maschinenspezifischen Blockgröße nb=128
erhalten.
Größte Leistungssteigerungen lassen sich durch Kombination aller Techniken - Aufrollen von Schleifen, Blockung und Kopieren von Blöcken - erreichen.
REAL, DIMENSION (qmax, qmax) :: a, b, c
REAL aa(nb, nb) ! Hilfsfeld
REAL t11, t21, t12, t22
c = 0
DO kk = 1, qmax, nb
kspan = MIN(nb, qmax-kk+1)
DO ii = 1, qmax, nb
ispan = MIN(nb, qmax-ii+1)
ilen = 2*(ispan/2) ! auf Gerade abrunden
DO i = ii, ii+ispan-1
DO k = kk, kk+kspan-1
aa(k-kk+1,i-ii+1) = a(i,k) ! transponiertes Kopieren
END DO
END DO
DO jj = 1, qmax, nb
jspan = MIN(nb, qmax-jj+1)
jlen = 2*(jspan/2)
DO j = jj, jj+jlen-1, 2 ! einfach aufgerollt
DO i = ii, ii+ilen-1, 2 ! einfach aufgerollt
t11 = 0.
t21 = 0.
t12 = 0.
t22 = 0.
DO k=kk, kk+kspan-1
t11 = t11 + aa(k-kk+1,i-ii+1)*b(k,j )
t21 = t21 + aa(k-kk+1,i-ii+2)*b(k,j )
t12 = t12 + aa(k-kk+1,i-ii+1)*b(k,j+1)
t22 = t22 + aa(k-kk+1,i-ii+2)*b(k,j+1)
END DO
c(i ,j ) = c(i ,j )+t11
c(i+1,j ) = c(i+1,j )+t21
c(i ,j+1) = c(i ,j+1)+t12
c(i+1,j+1) = c(i+1,j+1)+t22
END DO
END DO
END DO
END DO
END DO
Die beiden äußeren Schleifen der inneren Schleifenschachtelung
werden dabei einfach aufgerollt
|
"It should be clear however, that with a sufficiently
complex preprocessor, it is entirely possible to exactly
emulate any compiled language. Compilers are exactly this
kind of preprocessor." - |
Viele Programmtransformationen können auch von optimierenden Compilern automatisch durchgeführt werden. So steht z.B. auf HP-Workstations ein optimierender Präcompiler mit einer eigenen, BLAS-ähnlichen Vektor-Library zur Verfügung. Dieser erwähnte Präcompiler wandelt das bereits bekannte Beispiel
REAL, DIMENSION (qmax, qmax) :: a, b, c
c = 0
DO i = 1, qmax, 1
DO j = 1, qmax, 1
DO k = 1, qmax, 1
c(i,j) = c(i,j) + a(i,k)*b(k,j)
END DO
END DO
END DO
in den Aufruf
CALL blas_$sgemm('n','n',(m),(n),(k),0.,a(1,1),lda,b(1,1),ldb,1.,c(1,1),ldc)
um.Die Auswahl geeigneter Alghorithmusvarianten und das Fine-Tuning erfordert einen beträchtlichen Aufwand. Sodaß in den meisten Fällen das zurügreifen auf bereits vorhandene Bibliotheken, wo dies möglich und ausreichend ist, vorzuziehen ist.
Nachfolgend ein Beispiel für die Verwendung der physikalische
Berechnungen unterstützenden
C++-Bibliothek RHALE++:
void Decompose(const double delt, SymTensor& V,
Tesor& R, const Tesor& L)
{
Symtensor D = Sym(L);
AntiTensor W = Anti(L);
Vector z = Dual(V*D);
Vector omega = Dual(W) - 2.0*Inverse(V-Tr(V)*One)*z;
AntiTensor Omega = 0.5*Dual(omega);
R = Inverse(One-0.5*delt*Omega) * (One+0.5*delt*Omega)*R;
V += delt*Sym(L*V - V*Omega);
}
Die hier gezeigte Optimierungsverfahren sind stark von der zugrundeliegenden Rechnerarchitektur abhängig. Bei Hardware ist aber die Entwicklung kaum vorhersehbar. Möglicherweise wird durch den nächsten Technologiesprung vieles hier gezeigte unbedeutend und taucht erst mit dem darauf folgenden Technologie wieder aus der Versenkung auf.
Welche Programmiersprache wird in Zukunft im Bereich der numerischen
Berechnungen die Führung erhalten?
Nun, der Bereich der wissenschaftlichen und numerischen Berechnungen
ist relativ klein, wenn man ihn nach der Anzahl der in dieser
Richtung aktiven Programmierer beurteilt. Gleichzeitig haben Programme
aus diesem Bereich für viele anderen Gebiete große
Bedeutung.
Im Moment ist eine Entwicklung zu weiterentwickelten
Alghorithmen zu bemerken, von der Sprachen nur dann profitieren können,
wenn sie viele verschiedene Datenstrukturen effizient
unterstützen.
Werden Sprachen die sich im technischen Bereich bewährt haben,
wie C++ sich hier auch
durchsetzen? Allerdings müßten
hier die Compiler bessere Optimierungen für Probleme der
numerische Mathematik erhalten.
Oder gelingt es einer neueren
FORTRAN-Version
flexiblere Konzepte
und Paradigmen, wie Objektorientierung, Generizität, ...
zu unterstüzen?
Derzeit scheinen sich beide Entwicklungen abzuzeichnen, sodaß
man künftig mehr Auswahl an geeigneten Sprachen erwarten kann.
Falls Sie bisher keine Links weiterverfolgt haben, können Sie nun ebenfalls zu den restlichen Seiten weitergehen.
|
Gottes letzte Botschaft an die Menscheit:
"Wir entschuldigen uns für die Strapazen." - Macht's gut, und danke ... / |
Dies ist der aufbereitete Text zu