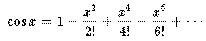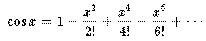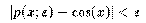[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]

Rundungsfehler

Auf jedem Computer stehen nur endlich viele Zahlen zur Verfügung. INTEGER- und Gleitpunktzahlen mit fester Stellenanzahl. Daher können die in einem Algorithmus auftretenden Rechenoperationen im allgemeinen nicht exakt ausgeführt werden; bei jedem Rechenschritt muß das Ergebnis auf eine der verfügbaren (meist auf eine der nächstgelegenen) Gleitpunktzahlen abgebildet - gerundet werden. Der Unterschied zwischen dem exakten Resultat und dem gerundeten Ergebnis einer Rechenoperation wird als Rundungsfehler (round-off error) oder Rechenfehler bezeichnet. Die Auswirkungen aller Rundungsfehler auf das Endergebnis des Näherungsverfahren bezeichenet man als Rundungsfehler- bzw. Rechenfehlereffekt.


Beispiel (Addition mit Gleitpunktzahlen)

In diesem Beispiel gehen wir von einem "gedachten" Computer mit 10er-Zahlensystem aus, der 5 Mantissenstellen speichern kann. Der Exponent darf von -127 bis 128 gehen.
Wir führen eine triviale Rechenoperation aus:

a + b = ? a = 1.2345E+00 b = 2.3456E-03 oder anders dargestellt:
a = 1.2345 b = 0.0023456 damit ist die (richtige) Summe: a + b = 1.2368456 Nun führen wir die gleiche Berechnung auf einem Computer, in Gleitkommarithmetrik durch: Wir bringen a und b zur Addition aufgleichen Exponenten: a = 1.2345000E+00 b = 0.0023456E+00 Hier haben wir bereits ein Problem: Um b exakt darstellen zu können müßte der verwendete Computer Mantissen mit 8 Stellen darstellen können, unser "hypothetischer" Computer kann aber nur 5 Mantissenstellen speichern. b wird also gerundet (das kommt noch genauer ...) b = 0.0024 a + b = 1.2369E+00 =1.2369 das richtige Resultat ist aber 1.2368456 (wie oben berechnet) Der Computer hat also falsch gerechnet (im streng mathematischen Sinn). Da die Ursache in der notwendigen Rundung liegt, wird dieser Fehler auch "Rundungsfehler-Effekt" genannt.

Beispiel (Kosinus-Reihe)
Das ist ein Beispiel wie es in der Praxis oft vorkommt:
Ein Mathematiker gibt einem Informatiker einen Algorithmus, damit der ihn implementiert. Im gegebenen Beispiel waren z.B. die Routinen für sin(x) und cos(x) zu ungenau. Der Informatiker will diese Kreisfunktionen also selbst genauer berechnen. (Tempo spielt keine Rolle, die Berechnung erfolgt sehr selten) Der Mathematiker hat die Taylorreihe vorgeschlagen.
Mit einem geeigneten Abbruchkriterium versehen, kann man die Reihenentwicklung

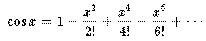\cos x = 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \frac{x^6}{6!} + \dots
in Algorithmen zur Berechnung der Kosinusfunktion verwenden. Auf Grund der Konvergenz der Taylorreihe für alle x [Element] [R] läßt sich für jedes Argument x und jedes [epsilon] > 0 ein k(x;[epsilon]) finden, das die geforderte Approximationsgenauigkeit

TODO

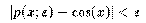
liefert. Das ist ein Ergebnis der Analysis, in der die Rechenoperationen im Bereich der reellen Zahlen vorausgesetzt werden ("exakte" Rechnung). Man kann sich leicht durch Implementierung des folgenden -Taylor- Polynom-Algorithmus überzeugen, daß diese Aussage nicht ohne Schwierigkeiten auf die Situation am Computer ubertragbar ist.

Nun hat der Informatiker den folgenden simplen Code zur Berechnung der Tailorreihe in Fortran90 implementiert:
(In Fortran90 liefert EPSILON(x) eine Schranke für den relativen Rundungsfehler des Gleitpunkt-Datentyps ihres Arguments (siehe Abschnitt 4.8)
kosinus = 0.; term = 1.; k2 = 0; xx = x*x DO WHILE (ABS(term) > ABS(kosinus)*EPSILON(kosinus)) kosinus = kosinus + term k2 = k2 + 2 term = (-term*xx)/REAL(k2*(k2-1)) END DO
Das File gibt es auch in C
Für x = 3.14159265 [ungefähr] PI liefert der Algorithmus (mit einfach genauer Maschinenarithmetrik) das in allen Stellen richtige Ergebnis
kosinus = -1.000000E+00.

Das gleiche Programm mit dem Wert 31.4159265 [ungefähr] 10[PI] liefert jedoch statt des erwarteten Resultates cos 10[PI] = 1 den für eine Funktion, deren Werte ausschließlich im Intervall [-1,1] liegen, völlig absurden Wert

kosinus = -8.593623E+04.

Die Ursache für das totale Versagen dieses Algorithmus liegt an den sogenannten "Auslöschungseffekten" (speziellen Effekten im Bereich der Rechenfehler), die für große Werte von x immer stärker werden:
Der Betrag der einzelnen Reihenterme wird im Fall x [etwa] 10[PI] zunächst bis
term = -( x^30 / 30! ) [etwa] -3.09*10^12
immer größer und nimmt von da an monoton ab (siehe Abb. 2.15). Dementsprechend treten sehr große Zwischensummen auf, obwohl das exakte Resultat im Intervall [-1,1] liegt. Bei der weiteren Summation tritt Auslöschung sämtlicher signifikanter Stellen ein. Also:
term(30) = -3.0962506*10^12 , das 30. Summenglied
term(60) = -8.1062036*10^7 , das 60. Summenglied
 auf gleichen Exponenten gebracht für die Addition:
-3.0962506*10^12 -0.0000811*10^12 durch die begrenzte Länge der Mantisse gehen ab der 3. Stelle alle Werte verloren = -3.0963317*10^12
Das Ergebnis der Reihenentwicklung ist von der Summationsreihenfolge abhängig!


Tatsächlich kann das Problem wesentlich schlimmer sein, die Summanden werden aufsummiert, die Summe kann wesentlich größer sein als der letzte Summand. Bei Reihenentwicklungen kann es zum Fall kommen, daß alle weitere Summenglieder, wenn sie auf gleichen Exponenten wie die bisherige Summe gebracht werden, zu
0.0000000*10^xx werden, also wegfallen.

Für unser Beispiel ergibt sich als ein möglicher Ansatz, die Summationsreihenfolge umzudrehen, also die kleinen Terme zuerst zu berechnen.

In der einschlägigen Fachliteratur werden Möglichkeiten aufgezeigt, Rundungsfehlereffekte abzuschtätzen. In der Praxishat sich gezeigt, daß diese Rundungsfehlerabschätzungen bei umfangreichen Algorithmen zu aufwendig sind und oft zu groß (pessimistische) Fehlerschranken liefern. Bei Verfahren mit einer großen Anzahl von Rechenoperationen ist im allgemeinen ein Kompensationseffekt der einzelnen Rundungsfehler zu beobachten, der jedoch bei den garantierten Fehlerschranken nicht berücksichtigt werden kann.

[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]